K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 9 2023
a)
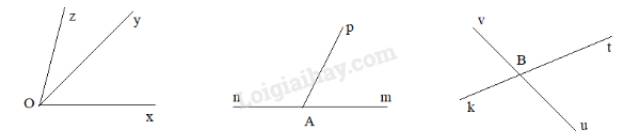
+ Ví dụ về 2 góc kề nhau: Góc xOy và góc yOz
+ Ví dụ về 2 góc kề bù: góc mAp và pAn
+ Ví dụ về hai góc đối đỉnh: góc uBt và góc vBk
b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
c)
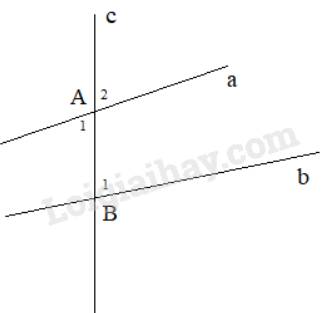
Đường thẳng c cắt hai đường thẳng a và b, tạo ra: Góc A1 và B1 là cặp góc so le trong; Góc A2 và B1 là cặp góc đồng vị
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau; hai góc so le trong bằng nhau ( Tính chất 2 đường thẳng song song)
e) Tiên đề Euclide về đường thẳng song song: Qua 1 điểm nằm ngoài đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
20 tháng 1 2016
em hoc lop sau nhung da co cau nay co giao giao de kho qua
22 tháng 8 2019
*Lời giải chi tiết:
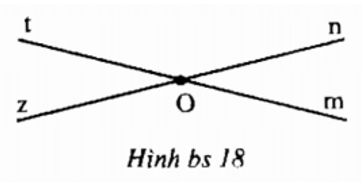
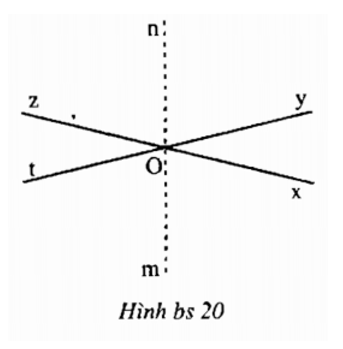
a) Vì góc nOt kề bù với góc mOn nên Ot là tia đối của tia Om. Tương tự, góc mOz kề bù với góc mOn nên Oz là hai tia đối của tia On. Từ đó, zOt và mOn là hai góc đối đỉnh.
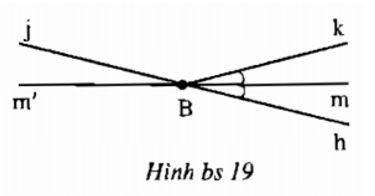
b) Vì góc kBj kề bù với góc hBk nên Bj là tia đối của tia Bh. Từ đó, m’Bj và hBm là hai góc đối đỉnh.
c) Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, zOy và tOx là hai góc đối đỉnh, tức là ∠zOy = ∠tOx.
Vì On, Om đều là tia phân giác và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180°.
Suy ra Om và On là hai tia đối nhau.
Từ đó, ∠zOn và ∠mOx là hai góc đối đỉnh.
NT
1
D
13 tháng 11 2023
mình chỉ có ngần này ví dụ thôi mong bạn thông cảm:))
CHÚC BẠN HỌC TỐT!!!!!!!!!!!
HF
28 tháng 9 2019
A B D E F C
Như hình vẽ trên: DE là pg góc ADB và DF là pg góc ADC
=>ADE = 1/2 (ADB) và ADF = 1/2(ADC)
=>ADE + ADF = EDF = 1/2(ADB + ADC) = 1/2*180 = 90
=>dpcm
28 tháng 9 2019
Giải:
O x' x y t m 0 t' GT xOy và x'Oy kề bù Ot là tia phân giác của góc xOy Ot' là tia phân giác của góc x'Oy KL Ot vuông góc với Ot'
Đặt \(\widehat{xOy}=m^0(0< m^0< 180^0)\)
Hai góc xOy và yOx' là hai góc kề bù nên \(\widehat{xOy}+\widehat{yOx'}=180^0\)do đó \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-m^0\)
Theo giả thiết Ot và Ot' lần lượt là tia phân giác của góc xOy và x'Oy nên \(\widehat{tOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}m^0\)và \(\widehat{t'Oy}=\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\left[180^0-m^0\right]\). Tia Oy nằm giữa hai tia Ot và Ot', do đó \(\widehat{tOt}=\widehat{tOy}+\widehat{yOt'}=\frac{1}{2}m^0+\frac{1}{2}\left[180^0-m^0\right]=90^0\)
Vậy \(Ot\perp Ot'\)
Hai góc kề bù là hai góc kề nhau và có tổng số đo là 180⁰
Trong hình trên, ∠xOy và ∠xOy' là hai góc kề bù
+ Hai góc kề bù là 2 góc vừa BÙ cho nhau và vừa KỀ cho nhau .
- Lý do hai góc kề bù có tổng số đo là 180 ĐỘ bởi vì hai góc bù nhau cũng có tổng số đo là 180 ĐỘ .
ngoài ra 2 góc kề bù cũng có thể có 1 cạnh trong chung nhưng không có điểm trong chung