Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
mà AD là phân giác
nên AEDF là hình thoi
mà \(\widehat{EAF}=90^0\)
nên AEDF là hình vuông
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{5}{7}\)
Do đó: DB=15/7(cm); DC=20/7(cm)
Vẽ hình(tự vẽ nha)
a) Ta có: \(BC^2\)=\(5^2=25\)
\(AB^2+AC^2=3^2+4^2=9+16=25\)
⇒\(AB^2+AC^2=BC^2\)
⇒Δ ABC vuông tại A (theo định lí Py-ta -go đảo)
⇒BA⊥AC
Mà DE//AC(gt);DF//AB(gt)
⇒DE⊥BA;DF⊥AC(t/c)
Xét tứ giác AEDF có \(\widehat{AFD}=90^o\left(DF\perp AC\right)\); \(\widehat{BAC}=90^o\left(BA\perp AC\right);\widehat{AED}=90^{o^{ }}\left(DE\perp BA\right)\);AD là p/g \(\widehat{BAC}\)
⇒Tứ giác AEDF là hình vuông (d/h)
b) Xét ΔABC có AD là tia phân giác \(\widehat{BAC}\),theo t/c ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\)⇒\(\dfrac{DC}{AC}=\dfrac{BD}{AB}\)hay\(\dfrac{DC}{4}=\dfrac{BD}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\dfrac{DC}{4}=\dfrac{BD}{3}\)=\(\dfrac{DC+BD}{4+3}=\dfrac{BC}{7}=\dfrac{5}{7}\)
\(\left\{{}\begin{matrix}DC=4.\dfrac{5}{7}=\dfrac{20}{7}\left(cm\right)\\BD=BC-DC=5-\dfrac{20}{7}=\dfrac{15}{7}\left(cm\right)\end{matrix}\right.\)
Bạn xem lại có phải chép sai đề không?,ở chỗ "tứ giác aebf là hình gì" và chỗ "af/ab+af/ab=1",và câu d có gì đó thiếu thiếu.Mk đã sửa lại câu a,vì như vậy mới ra tứ giác.

a, BC sử dụng py ta go : => BC = 29
b, AD là p/g => BD/DC = AB / AC = 20/21
=> BD /20 = DC/21 = BD+DC / 20 + 21 = 29/41
=> BD = 29/41 . 20 = 580/41
=> DC = 29/41 . 21 = 609/41
b, AB// DF
AB vg AC
=> DF vuông góc với AC
DE // AC
AB vg AC
=> DE vg AB
tg AFDE có ba giocs vuông => AFDE là HCN
Sử dụng ta let thì phải

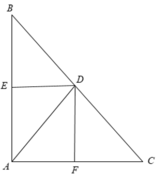

A B C D H E F
a. ta có: AD là phân giác góc A
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}\)
\(\Leftrightarrow\dfrac{3}{4}=\dfrac{BC-DC}{DC}\)
\(\Leftrightarrow\dfrac{3}{4}=\dfrac{5}{DC}-1\)
\(\Leftrightarrow\dfrac{7}{4}=\dfrac{5}{DC}\)
\(\Leftrightarrow7DC=20\Leftrightarrow DC=\dfrac{20}{7}\)
\(DB=BC-DC=5-\dfrac{20}{7}=\dfrac{15}{7}\)
b. ta có:\(AH.BC=AB.AC\)
\(\Leftrightarrow5AH=12\Leftrightarrow AH=\dfrac{12}{5}\)
áp dụng định lý pitago vào tam giác vuông ABH:
\(\Rightarrow BH=\sqrt{3^2-\left(\dfrac{12}{5}\right)^2}=\dfrac{9}{5}\)
HD=BD - BH = \(\dfrac{15}{7}-\dfrac{9}{5}=\dfrac{8}{5}\)
\(S_{ADH}=\dfrac{1}{2}.AH.HD=\dfrac{1}{2}.\dfrac{12}{5}.\dfrac{8}{5}=\dfrac{48}{25}cm^2\)
c. tứ giác AEDF là hình chữ nhật vì có 3 góc vuông