Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước sóng dài nhất của vạch quang phổ trong dãy Lai-man thu được khi nguyên tử nhảy từ L về K. Khi đó \(\lambda_1\) thỏa mãn: \(hf_1=\frac{hc}{\lambda_1}= E_2-E_1,(1)\)
Bước sóng \(\lambda_2\)của vạch kề với \(\lambda_1\) thu được khi nguyên tử nhảy từ M về K.
Khi đó \(\lambda_2\) thỏa mãn: \(hf_2=\frac{hc}{\lambda_2}= E_3-E_1,(2)\)
Bước sóng \(\lambda_{\alpha}\) trong vạch quang phổ \(H_{\alpha}\) trong dãy Ban-me thu được khi nguyên tử nhảy từ M về L.
Khi đó \(\lambda_{\alpha}\) thỏa mãn: \(hf_{\alpha}=\frac{hc}{\lambda_{\alpha}}= E_3-E_2,(3)\)
Trừ (2) cho (1) thu được (3):
\(\frac{hc}{\lambda_{2}}-\frac{hc}{\lambda_{1}}= \frac{hc}{\lambda_{\alpha}}\)=> \( \frac{1}{\lambda_{\alpha}}=\frac{1}{\lambda_{2}}-\frac{1}{\lambda_{1}}\)
=> \(\lambda_{\alpha}=\frac{\lambda_1\lambda_2}{\lambda_1-\lambda_2}.\)

\(x_s= k\frac{\lambda D}{a}.\)
\(d_2-d_1 = \frac{x_sa}{D}= k\lambda\)
=>\(k= \frac{d_2-d_1}{\lambda}=\frac{1,5.10^{-6}}{\lambda}.(1)\)
Thay các giá trị của bước sóng \(\lambda\)1, \(\lambda\)2,\(\lambda\)3 vào biểu thức (1) làm sao mà ra số nguyên thì đó chính là vân sáng của bước sóng đó.

Bước sóng dài nhất trong quang phổ Banmel sẽ là bước sóng ứng với bước chuyển từ 3 xuống 2
\(E=\frac{hc}{\lambda}=E_3-E_2=A\text{/}4-A\text{/}9\)
\(\Rightarrow A=2,18.10^{-19}J\)
Mình không hiểu câu hỏi của bạn lắm nhưng theo mình đoán bước sóng ngắn nhất này sẽ từ \(\text{n=∞ }\)
đến n=1
Năng lượng sẽ đúng bằng A
\(\lambda=\text{91,1528nm }\)

Ta có
Wđ= \(\frac{hc}{\lambda}\)
lấy tỉ lệ
1,5=\(\frac{hc}{1.2\lambda}\) => \(\lambda\)
sau đó A=\(\frac{hc}{\lambda}\)
không biết có đúng không. Nếu sai sót mong mn góp ý ạ![]()

Đáp án: A
Vạch đỏ ứng với sự chuyển mức năng lượng từ M L:
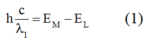
Vạch lam ứng với sự chuyển mức năng lượng từ N ® L:
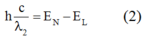
Vạch có bước sóng dài nhất trong dãy Pa-sen ứng với sự chuyển mức năng lượng từ N ® M. Trừ vế với vế của (2) và (1) ta có:
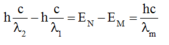
Từ đó ta có:
![]()

Phương trình sóng tổng quát \(u=a\cos2\pi( ft-\frac{x}{\lambda})\)
So sánh với phương trình bài cho => \(\lambda=50cm.\)
2 vạch \(\alpha\) và \(\beta\) do bước chuyển tử mức 3-2 và 4-2
Bước sóng dài nhất trong dãy Pasen là từ 4 xuống 3
\(E_{43}=E_{42}-E_{32}\)
\(\frac{hc}{\lambda}=\frac{hc}{\lambda\beta}-\frac{hc}{\lambda\alpha}\)
\(\frac{1}{\lambda}=\frac{1}{\lambda\beta}-\frac{1}{\lambda\alpha}\)