Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)tam giác BHA có BI là phân giác(góc ABI=góc HBI) nên \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow AI\cdot BH=AB\cdot IH\)
b)xét tam giác BHA và tam giác BAC có:
góc ABC chung
góc BHA=góc BAC=90 độ
\(\Rightarrow\Delta BHA\infty\Delta BAC\left(g.g\right)\\ \Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow AB^2=BH\cdot BC\)
c)ta có:
theo câu a) \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow\dfrac{IH}{AI}=\dfrac{BH}{AB}\left(1\right)\)
theo câu b) \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
ta lại có BD là phân giác góc ABC nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{AD}{DC}=\dfrac{BH}{AB}\)(2)
từ (1) và (2)\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(=\dfrac{BH}{AB}\right)\)

a: Xét tứ giác AECF có
AF//EC
AF=EC
Do đó: AECF là hình bình hành
b: Xét tứ giác ABEF có
AF//BE
AF=BE
Do đó: ABEF là hình bình hành
mà AF=AB
nên ABEF là hình thoi
Suy ra: AE\(\perp\)BF
c: \(\widehat{ABD}=180^0-60^0=120^0\)
e: Xét tứ giác FDCE có
FD//CE
FD=CE
Do đó: FDCE là hình bình hành
ma FD=CD
nên FDCE là hình thoi
=>FC là đường trung trực của DE
hay E và D đối xứng nhau qua FC

Câu 4:Giaỉ:
+) Gọi số ngày làm theo dự định là x (ngày ) (x:nguyên,dương)
Khi đó số ngày làm trên thực tế là x-2 (ngày)
+) Số sản phẩm làm được theo kế hoạch gọi là 120x (sản phẩm)
Số sản phẩm làm được theo thực tế là 130(x-2) (sản phẩm)
Vì trên thực tế số sản phẩm làm được bằng số sản phẩm dự định nên ta có:
120x= 130(x-2)
<=>120x -130x= -260
<=> -10x= -260
=> x= \(\dfrac{-260}{-10}=26\left(TMĐK\right)\)
Vậy: Số sản phẩm xí nghiệp đã sản xuất là: 26.120= 3120 (sản phẩm)

Bài 1:
\(A=3-x^2\)
Với mọi giá trị của x ta có:
\(x^2\ge0\Rightarrow3-x^2\le3\)
Vậy MAx A = 3
Để A = 3 thì \(x=0\)
\(B=4x-x^2+3=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7\)
Với mọi giá trị của x ta có:
\(\left(x-2\right)^2\ge0\Rightarrow-\left(x-2\right)^2\le0\)
\(\Rightarrow-\left(x-2\right)^2+7\le7\)
Vậy Max B = 7
Để B = 7 thì \(x-2=0\Rightarrow x=2\)
\(C=x-x^2=-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\)
Với mọi giá trị của x ta có:
\(\left(x-\dfrac{1}{2}\right)^2\ge0\Rightarrow-\left(x-\dfrac{1}{2}\right)^2\le0\)
\(\Rightarrow-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
Vậy Max C = \(\dfrac{1}{4}\)
Để C = \(\dfrac{1}{4}\) thì \(x-\dfrac{1}{2}=0\Rightarrow x=\dfrac{1}{2}\)
\(D=\dfrac{1}{x^2+2x+3}=\dfrac{1}{\left(x+1\right)^2+2}\)
Với mọi giá trị của x ta có:
\(\left(x+1\right)^2\ge0\Rightarrow\left(x+1\right)^2+2\ge2\)
\(\Rightarrow\dfrac{1}{\left(x+1\right)^2+2}\le\dfrac{1}{2}\)
Vậy Max D= \(\dfrac{1}{2}\)
Để \(D=\dfrac{1}{2}\) thì \(x+1=0\Rightarrow x=-1\)

Câu 4:
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
b: \(A=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2}{2x\left(x+5\right)}+\dfrac{2\left(x^2-25\right)}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
c: Để A=-3 thì x-1=-6
hay x=-5(loại)

Tìm GTNN:
a. M = x2 - 8x + 5
M = ( x^2 - 2.x.4 + 16 ) - 11
M = ( x- 4 )^2 -11
Vì ( x- 4 )^2 > hoặc = 0 vs mọi x
=> ( x-4)^2 -11 > hoặc = -11 vs mọi x
=> M > hoặc = -11 vs mọi x
Vậy min M = -11 <=> ( x- 4 )^2 = 0
<=> x = 4
a, A = x2 - 6x + 10
A=( x^2 - 2.x.3+9 ) +1
A = ( x- 3 )2 +1
Thay x= 103
A = ( 103 - 3 )2 +1
= 100^2 + 1 = 10000+ 1 = 10001
b, B = x2 -10x + 25
B = x^2 - 2.x.5 + 52
B = ( x- 5 )2
Thay x = 25
B = ( 25 - 5 )2
B = 20^2 = 400

Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

2. Viết hạng tử thích hợp vào dấu * để mỗi đa thức sau trở thành bình phương của một tổng hoặc một hiệu.
a) \(25x^2+\cdot\cdot\cdot+81\)
\(=\left(5x\right)^2+...+9^2\)
\(=\left(5x\right)^2+2.5x.9+9^2\)
\(=25x^2+90x+81\)
b) \(64x^2-\cdot\cdot\cdot+9\)
\(=\left(8x\right)^2-\cdot\cdot\cdot+3^2\)
\(=\left(8x\right)^2-2.8x.3+3^2\)
\(=64x^2-48x+9\)
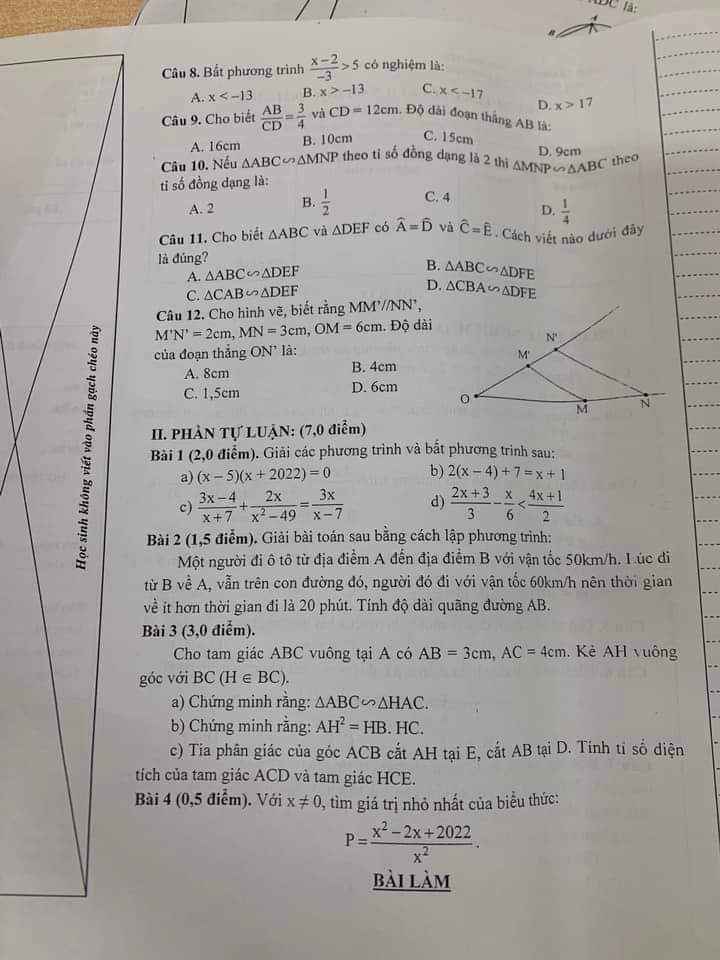
 cac
cac
 giai dum bai nay voi ak e dang can gap
giai dum bai nay voi ak e dang can gap



Bài 4:
\(P=\dfrac{x^2-2x+2022}{x^2}=\dfrac{2022x^2-2.2022x+2022^2}{2022x^2}=\dfrac{\left(x^2-2.2022x+2022^2\right)+2021x^2}{2022x^2}=\dfrac{\left(x-2022\right)^2}{2022x^2}+\dfrac{2021}{2022}\ge\dfrac{2021}{2022}\)\(P_{min}=\dfrac{2021}{2022}\Leftrightarrow x=2022\)