
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a,\\ \left\{{}\begin{matrix}x< 1.hoặc.x>2\\\dfrac{2x^2-3x-2}{3x+1}\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 1.hoặc.x>2\\x\le\dfrac{-1}{2}.hoặc.\dfrac{-1}{3}< x< 1\end{matrix}\right.\\ \Rightarrow x\le-\dfrac{1}{2}.hoặc.-\dfrac{1}{3}< x< 1\)
\(b,\\ \left\{{}\begin{matrix}x< -4.hoặc.x>1\\\dfrac{2x+1}{2x^2-5x+2}\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< -4.hoặc.x>1\\x\le-\dfrac{1}{2}hoặc.\dfrac{1}{2}< x< 2\end{matrix}\right.\\ \Rightarrow x< -4.hoặc.1< x< 2\)



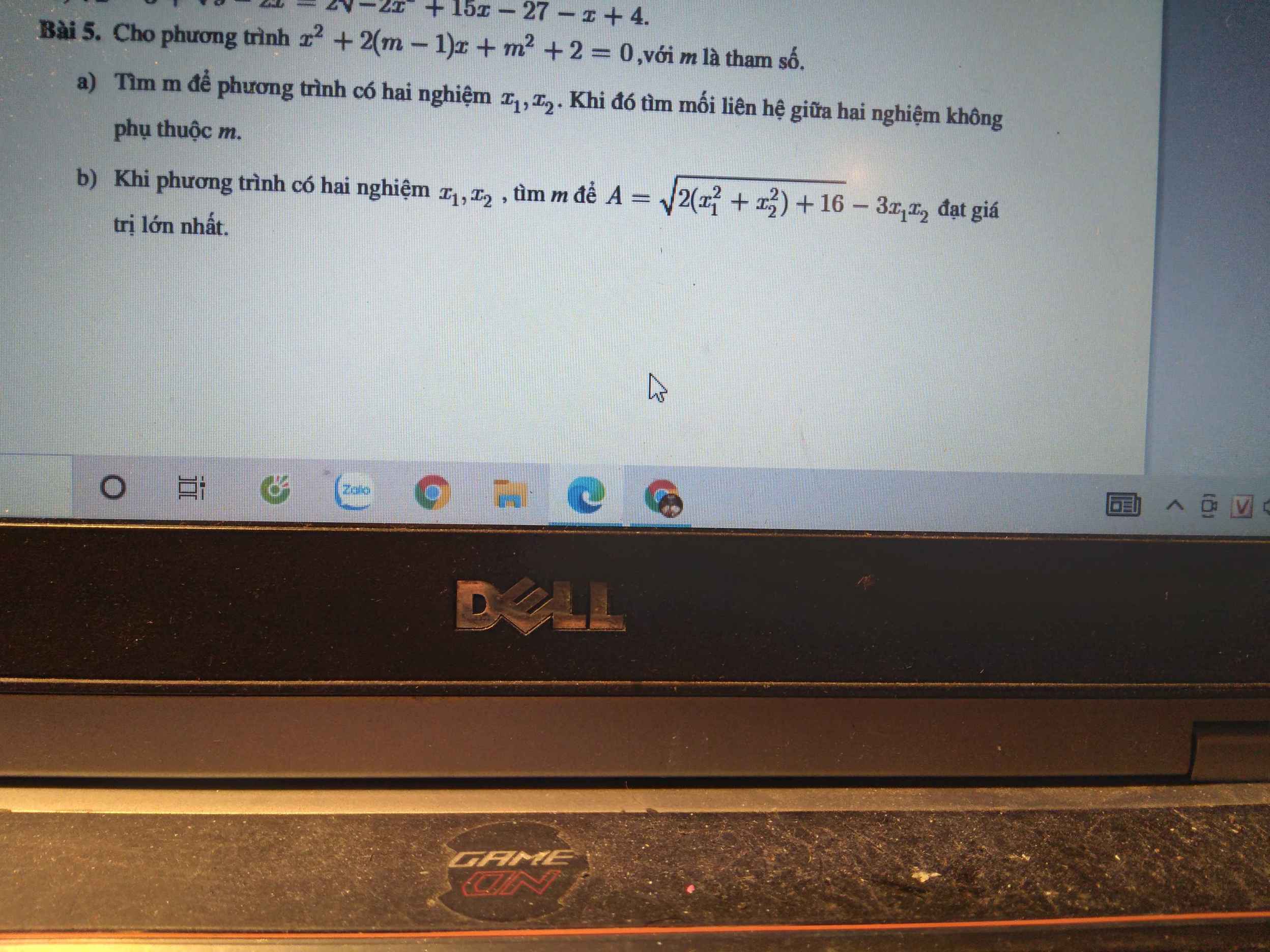
\(\Delta'=\left(m-1\right)^2-\left(m^2+2\right)=-2m-1\ge0\Rightarrow m\le-\dfrac{1}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2+2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_1+x_2+2}{2}=m\\x_1x_2-2=m^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{x_1+x_2+2}{x}\right)^2=m^2\\x_1x_2-2=m^2\end{matrix}\right.\)
\(\Rightarrow\left(\dfrac{x_1+x_2+2}{2}\right)^2=x_1x_2-2\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
b.
\(A=\sqrt{2\left(x_1+x_2\right)^2-4x_1x_2+16}-3x_1x_2\)
\(=\sqrt{8\left(m-1\right)^2-4\left(m^2+2\right)+16}-3\left(m^2+2\right)\)
\(=\sqrt{4m^2-16m+16}-3\left(m^2+2\right)\)
\(=\sqrt{\left(4-2m\right)^2}-3m^2-6\)
\(=\left|4-2m\right|-3m^2-6\)
\(=4-2m-3m^2-6\) (do \(m\le-\dfrac{1}{2}\Rightarrow4-2m>0\))
\(=-3m^2-2m-2\)
\(=-\dfrac{1}{4}\left(12m^2+8m+1\right)-\dfrac{7}{4}\)
\(=-\dfrac{1}{4}\left(6m+1\right)\left(2m+1\right)-\dfrac{7}{4}\le-\dfrac{7}{4}\)
\(A_{max}=-\dfrac{7}{4}\) khi \(m=-\dfrac{1}{2}\)

Bài 1:
Do d đi qua A nên phương trình d có dạng:
\(a\left(x-2\right)+b\left(y-5\right)=0\Leftrightarrow ax+by-2a-5b=0\) (1) với \(a^2+b^2>0\)
Áp dụng công thức khoảng cách:
\(d\left(I;d\right)=\dfrac{\left|a.4+b.1-2a-5b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|2a-4b\right|=2\sqrt{a^2+b^2}\)
\(\Leftrightarrow\left|a-2b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow a^2-4ab+4b^2=a^2+b^2\)
\(\Leftrightarrow3b\left(3b-4a\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\b=\dfrac{4a}{3}\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow\left[{}\begin{matrix}ax+0.y-2a-5.0=0\\ax+\dfrac{4a}{3}.y-2a-5.\dfrac{4a}{3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\3x+4y-26=0\end{matrix}\right.\)
Bài 2:
Bài này có nhiều cách làm, (ví dụ viết phương trình đường thẳng d, tính khoảng cách tới A và B rồi cho chúng bằng nhau, từ đó suy ra tương tự câu a), hoặc đơn giản hơn là lý luận như sau:
Đường thẳng d cách đều 2 điểm AB khi nó thỏa mãn 1 trong 2 trường hợp sau:
TH1: d song song AB
Ta có \(\overrightarrow{AB}=\left(-2;8\right)=2\left(-1;4\right)\Rightarrow d\) nhận (4;1) là 1 vtpt (do d song song AB)
Phương trình d có dạng:
\(4\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow4x+y+5=0\)
TH2: d đi qua trung điểm của AB
Gọi M là trung điểm AB, theo công thức trung điểm ta có \(M\left(4;3\right)\Rightarrow\overrightarrow{IM}=\left(6;0\right)=6\left(1;0\right)\)
\(\Rightarrow\) Đường thẳng d (hay IM) nhận (0;1) là 1 vtpt
Phương trình: \(0\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow y-3=0\)

Bài 6:
b: x+3y-6=0
=>x+3y=6
=>3y=6-x
=>y=-1/3x+2
Vì (d) vuông góc với y=-1/3x+2 nên -1/3a=-1
=>a=3
Vậy: (d): y=3x+b
Thay x=2 và y=5 vào (d), ta được:
b+6=5
hay b=-1

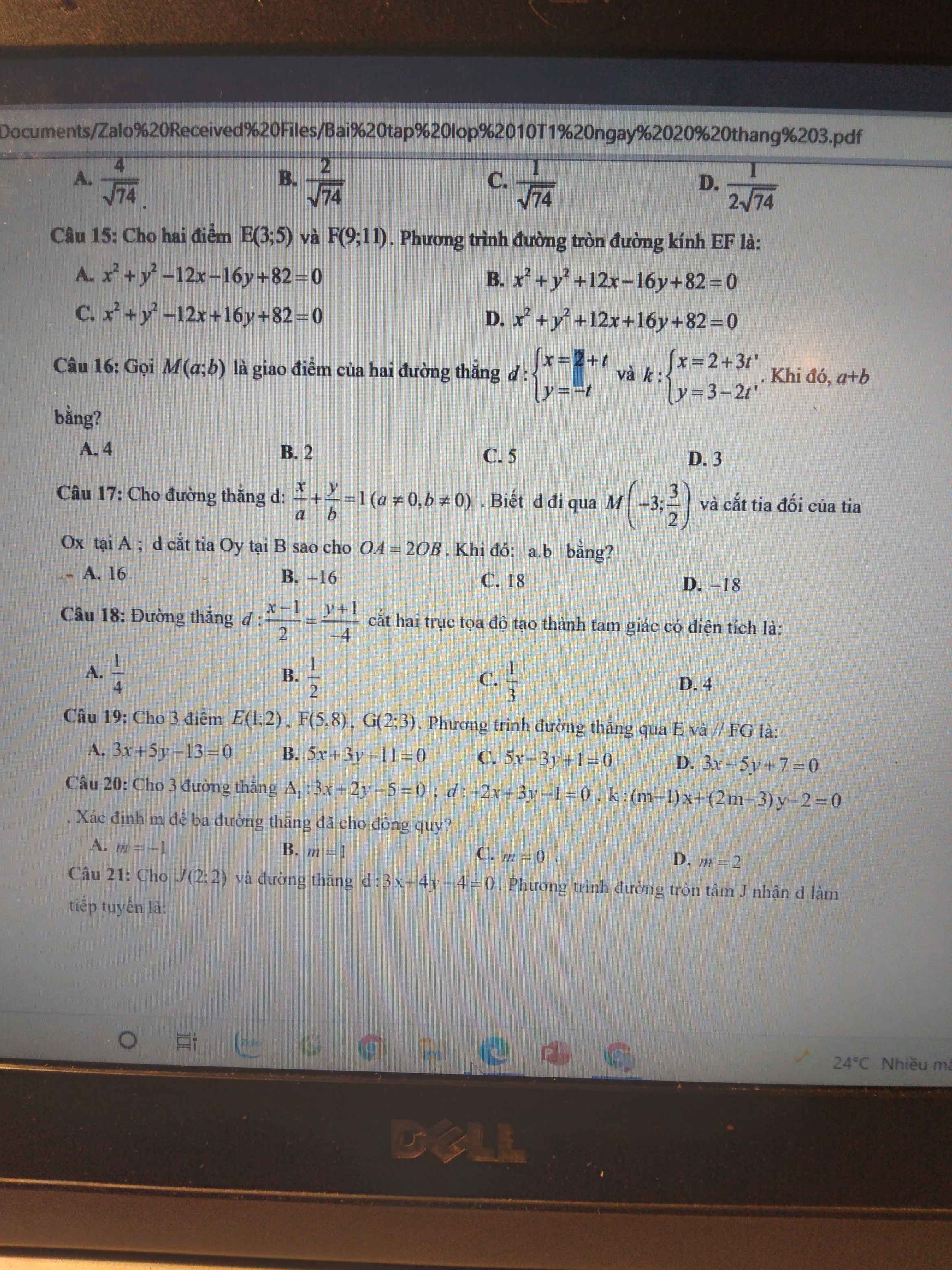
16.
Hệ tọa độ giao điểm: \(\left\{{}\begin{matrix}2+t=2+3t'\\-t=3-2t'\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}t=-9\\t'=-3\end{matrix}\right.\)
Thay \(t=-9\) vào pt d ta được: \(\left\{{}\begin{matrix}a=-7\\b=9\end{matrix}\right.\)
\(\Rightarrow a+b=2\)
17.
Do d qua M nên: \(\dfrac{-3}{a}+\dfrac{3}{2b}=1\) (1)
d cắt tia đối Ox tại A \(\Rightarrow a< 0\) và \(OA=-a\)
d cắt Oy tại b \(\Rightarrow b>0\) và \(OB=b\)
\(OA=2OB\Rightarrow-a=2b\)
Thế vào (1): \(\dfrac{-3}{a}+\dfrac{3}{-a}=1\Rightarrow a=-6\Rightarrow b=\dfrac{-a}{2}=3\)
\(\Rightarrow ab=-18\)
18.
Gọi A là giao điểm của d với Ox
\(\Rightarrow y_A=0\Rightarrow\dfrac{x_A-1}{2}=\dfrac{0+1}{-4}\Rightarrow x_A=\dfrac{1}{2}\)
\(\Rightarrow OA=\left|x_A\right|=\dfrac{1}{2}\)
Gọi B là giao điểm của d với Oy
\(\Rightarrow x_B=0\Rightarrow\dfrac{0-1}{2}=\dfrac{y_B+1}{-4}\Rightarrow y_B=1\)
\(\Rightarrow OB=\left|y_B\right|=1\)
\(S=\dfrac{1}{2}OA.OB=\dfrac{1}{4}\)

a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
![]()
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.
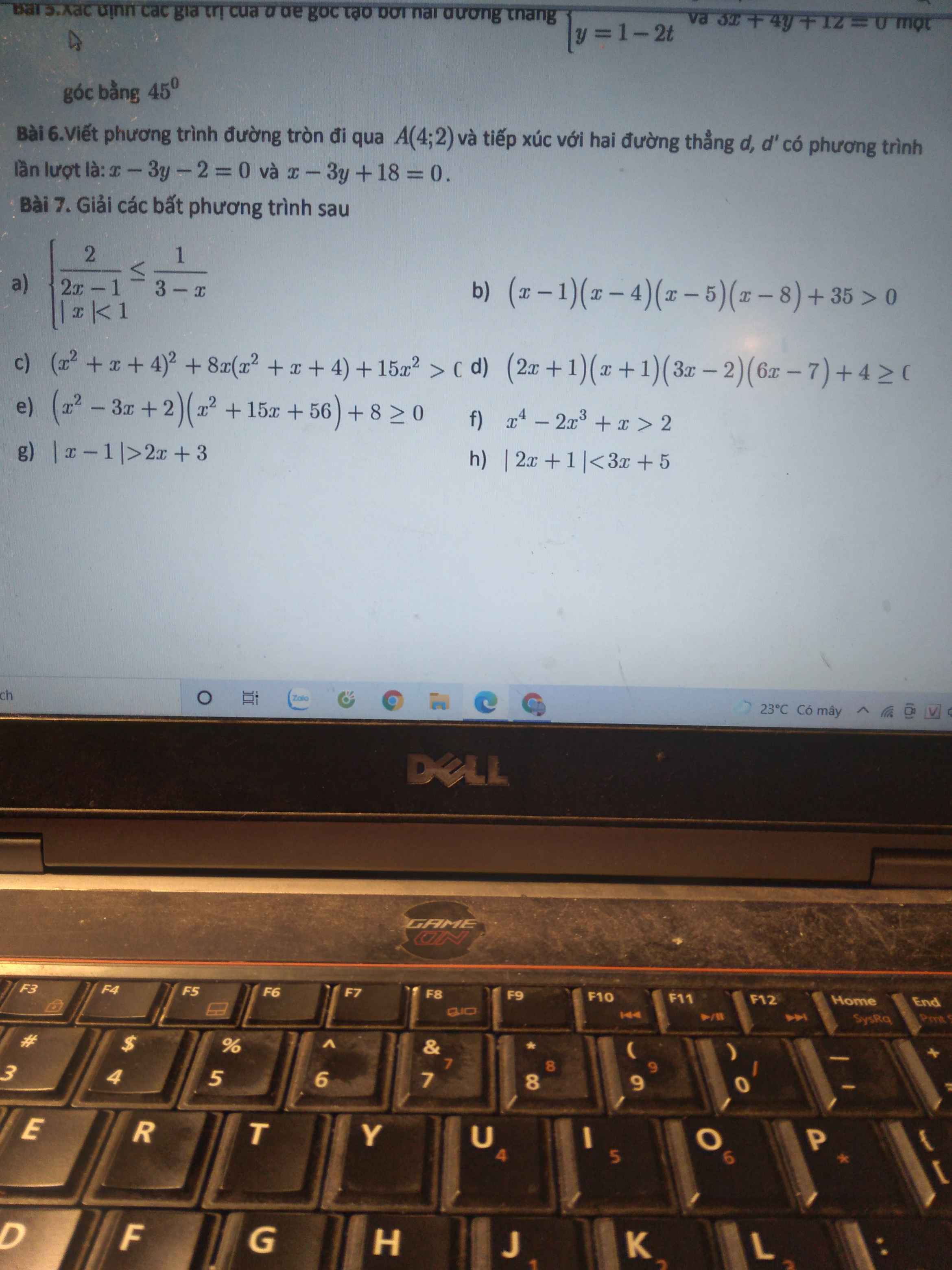








\(\left(x\ne3;x\ne\dfrac{1}{2}\right)\)\(\left\{{}\begin{matrix}\dfrac{2}{2x-1}\le\dfrac{1}{3-x}\\\left|x\right|< 1\Leftrightarrow-1< x< 1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2\left(3-x\right)-2x+1}{\left(2x-1\right)\left(3-x\right)}\le0\left(1\right)\\-1< x< 1\end{matrix}\right.\)\(\)
\(\left(1\right)\Leftrightarrow\dfrac{-4x+7}{\left(2x-1\right)\left(3-x\right)}\le0\)\(\Leftrightarrow\dfrac{-4x+7}{-2x^2+7x-3}\le0\Leftrightarrow x\in\left(-\infty;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(kết\) \(hợp:-1< x< 1\)\(\Rightarrow x\in\left(-1;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(b,\)\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)+35>0\)
\(\Leftrightarrow\left(x^2-9x+8\right)\left(x^2-9x+20\right)+35>0\)
\(đặt:x^2-9x+8=t\ge-\dfrac{49}{4}\)
\(bpt\Leftrightarrow t\left(t+12\right)+35>0\Leftrightarrow t^2+12t+35>0\Leftrightarrow\left[{}\begin{matrix}t< -7\\t>-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-9x+8< -7\\x^2-9x+8>-5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{9-\sqrt{21}}{2}< x< \dfrac{9+\sqrt{21}}{2}\\x\in\left(-\infty;\dfrac{9-\sqrt{29}}{2}\right)\cup\left(\dfrac{9+\sqrt{29}}{2};+\infty\right)\end{matrix}\right.\)
\(c;\)\(\left(x^2+x+4\right)^2+2.4x\left(x^2+x+4\right)+16x^2-x^2>0\)
\(\Leftrightarrow\left(x^2+x+4+4x\right)^2-x^2>0\)
\(\Leftrightarrow\left(x+2\right)^2\left(x^2+6x+4\right)>0\)
\(\Leftrightarrow x^2+6x+4>0\Leftrightarrow....\)
ý d; giống ý b
\(e;bpt\Leftrightarrow\left(x-2\right)\left(x-1\right)\left(x+7\right)\left(x+8\right)+8>0\)
\(\Leftrightarrow\left(x^2+6x-16\right)\left(x^2+6x-7\right)+8>0\)
\(đặt:x^2+6x-7=t\ge-16\Rightarrow t\left(t-9\right)+8>0\)
(làm giống ý b)
\(f;x^4-2x^3+x-2>0\Leftrightarrow\left(x+1\right)\left(x-2\right)\left(x^2-x+1\right)>0\left(do:x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\right)\)
\(\Rightarrow bpt\Leftrightarrow\left(x+1\right)\left(x-2\right)>0\Leftrightarrow\left[{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\)
\(g;h\) dùng bảng phá giá trị tuyệt đối để làm