K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 12 2021
\(2x^2+5xy+3y^2\\= 2x^2+2xy+3xy+3y^2\\= 2x\left(x+y\right)+3y\left(x+y\right)\\=\left(2x+3y\right)\left(x+y\right) \)
27 tháng 12 2021
2x^2-5xy-3y^2
= 2^x + xy - 6xy - 3y^2
= x(2x + y) - 3y(2x + y)
= (2x + y)(x - 3y)
LT
0
PH
0
PT
1
CM
19 tháng 9 2018
Đặt m = y2 .Điều kiện m ≥ 0
Ta có: y 4 – 1,16 y 2 + 0,16 =0 ⇔ m 2 -1,16m + 0,16 =0
Phương trình m 2 -1,16m + 0,16 = 0 có hệ số a = 1, b = -1,16, c = 0,16 nên có dạng a + b + c = 0
suy ra: m 1 = 1 , m 2 = 0,16
Ta có: y 2 =1 ⇒ y = ± 1
y 2 =0,16 ⇒ y = ± 0,4
Vậy phương trình đã cho có 4 nghiệm : y 1 =1 ; y 2 =-1 ; y 3 =0,4 ; y 4 =-0,4
CM
2 tháng 6 2018
Cộng vế với vế của từng phương trình với nhau ta được:
( x 3 + 3 x 2 + x – 5 ) + ( y 3 + 3 y 2 + y – 5 ) + ( z 3 + 3 z 2 + z – 5 ) = 0
( x – 1 ) ( x 2 + 4 x + 5 ) + ( y – 1 ) ( y 2 + 4 y + 5 ) + ( z – 1 ) ( z 2 + 4 z + 5 ) = 0 ( 1 )
Nếu x > 1 ⇒ z 3 + 3 z 2 + z – 5 > 1 ⇔ ( z – 1 ) ( z 2 + 4 z + 5 ) > 0 ⇒ z > 1
Tương tự với z > 1 ⇒ y > 1
Suy ra VT (1) > 0 (phương trình vô nghiệm)
Chứng minh tương tự với x < 1 ta cũng được phương trình (1) vô nghiệm
Suy ra phương trình (1) có nghiệm duy nhất x = y = z = 1
Đáp án:D
5 tháng 5 2020
Gọi x1,x2 là các nghiệm của phương trình đã cho
Áp dụng hệ thức Vi-et,ta có :
x1 + x2 = -5 ; x1x2 = -1
gọi y1,y2 là các nghiệm của phương trình phải lập,ta được :
y1 + y2 = x14 + x24 , y1y2 = x14x24
Ta có : x12 + x22 = ( x1 + x2 )2 - 2x1x2 = 25 + 2 - 27
Do đó : y1 + y2 = x14 + x24 = ( x12 + x22 )2 - 2x12x22 = 729 - 2 = 727
y1y2 = ( x1x2 )4 = 1
Từ đó pt phải lập có dạng : y2 - 727y + 1 = 0
5 tháng 5 2020
Ta co: P = -1 <0
=> (1) có 2 nghiệm phân biệt khác dấu
Gọi hai nghiệm đó là \(x_1;x_2\)
=> \(x_1+x_2=-5;x_1.x_2=-1\)
Ta có: \(\left(x_1.x_2\right)^4=\left(-1\right)^4=1\)
\(\left(x_1\right)^4+\left(x_2\right)^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2\)
\(=\left[\left(-5\right)^2-2.\left(-1\right)\right]^2-2.\left(-1\right)^2\)
\(=727\)
=> Phương trình có các nghiệm lũy thừa bậc 4 của các nghiệm phương trình (1) là:
\(x^2-727x+1=0\)
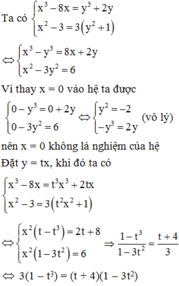
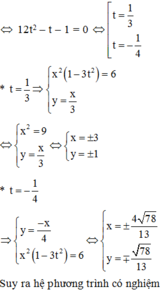
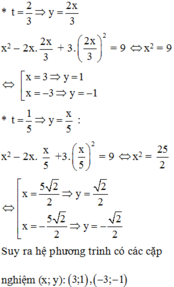
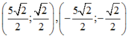
\(x^4+y^4=3y^2+1\Leftrightarrow-y^4+3y^2+1=x^4\ge0\)
\(\Rightarrow-y^4+3y^2+1\ge0\Rightarrow\frac{3-\sqrt{13}}{2}\le y^2\le\frac{3+\sqrt{13}}{2}\)
Mà \(y\in Z\Rightarrow y^2\)là số chính phương \(\Rightarrow y^2=0;1\)
*\(y^2=0\Rightarrow x^4=1\Rightarrow x=-1;1\)
*\(y^2=1\Rightarrow x^4+1=3+1\Rightarrow x^4=3\Rightarrow x\notin Z\)
Vậy phương trình có nghiệm nguyên \(\left(-1;0\right),\left(1;0\right)\)