Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(3+3^2+3^3+...+3^{60}\\ =\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{59}+3^{60}\right)\\ =\left(1+3\right)\left(3+3^3+...+3^{59}\right)\\ =4\left(3+3^3+...+3^{59}\right)⋮4\\ 3+3^2+3^3+...+3^{60}\\ =\left(3+3^2+3^3\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\\ =3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\\ =\left(1+3+3^2\right)\left(3+3^4+...+3^{58}\right)\\ =13\left(3+3^4+...+3^{58}\right)⋮13\)

ai giải hộ vs
tính giá trị của biểu thức sau: 2+22+23+24+....+215-216 cánh giải lun nha(không được sử dụng máy tính)

Bạn muốn tính toán giá trị của E hay muốn so sánh E với một số khác?
chứng minh rằng 1 phần 2 mũ 2 cộng 1 phần 3 mũ 2 + 1 4 mũ 2 chấm chấm chấm 1 phần 100 mũ 2 nhỏ hơn 1


Đặt A= \(\frac{1}{2}\)-\(\frac{1}{2^2}\)+\(\frac{1}{2^3}\)-\(\frac{1}{2^2}\)+....+\(\frac{1}{2^2}\)
=> 2A=1-\(\frac{1}{2}\)+\(\frac{1}{2^2}\)-\(\frac{1}{23}\)+...+\(\frac{1}{2^{98}}\)
=> 2A+A=1+\(\frac{1}{2^{99}}\)
=> 3A=1+\(\frac{1}{2^{99}}\)
=> A= \(\frac{1}{3}\)+\(\frac{1}{3.2^{99}}\)

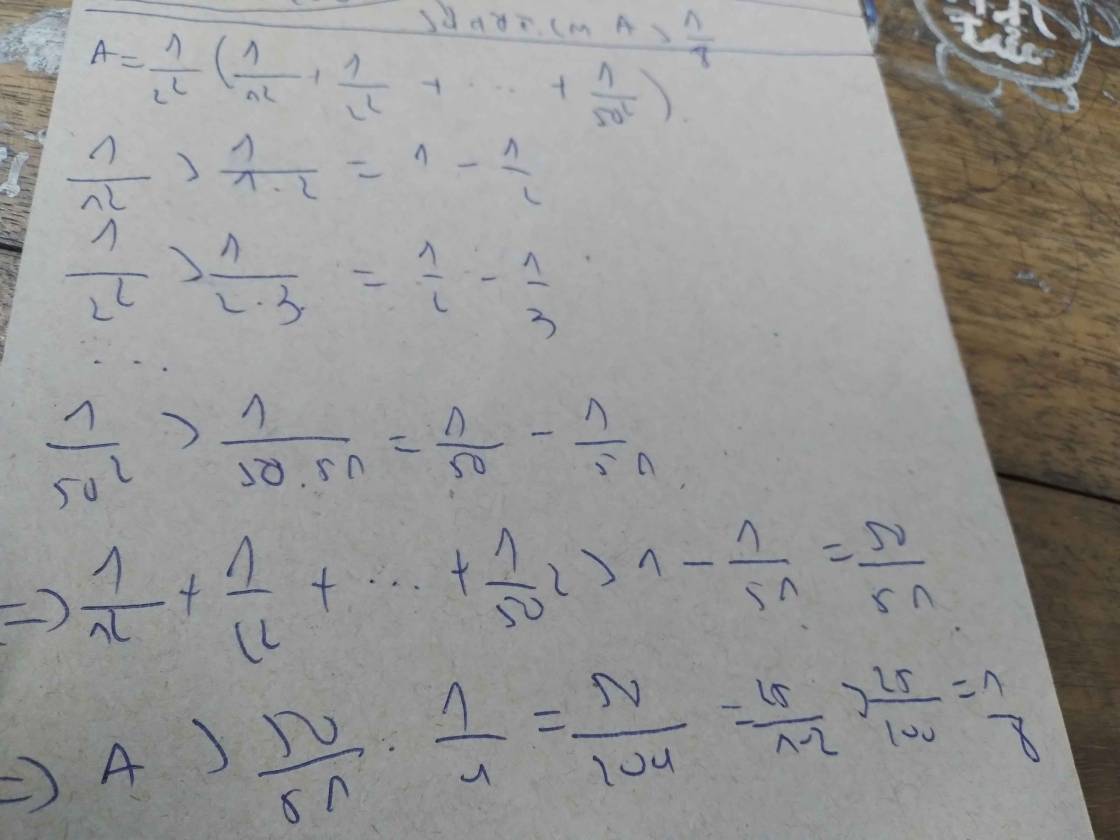
B=2+22+23+...+2100
2B=22+23+24+...+2101
2B-B=(22+23+24+...+2101)-(2+22+23+...+2100)
B=2101-2
Theo như đề bài thì B+2=2X mà B=2101-2
Vậy B+2=2101-2+2=2101=2x
Suy ra x=101
Đáp số 101