Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi chữ số ban đầu là ab ( a, b là STN. a#0 a=3b )
Nếu đổi chỗ 2 chữ số của số đó thì được số mới là: ba
Theo bài ra ta có:
ba - ab = 54
=> 10b+a-10a-b=54
=> 9b-9a=54
=) 9(b-a)=54
=> b-a=4
Vì a=3b => Số ab là 93
học tốt
Ta có các số tự nhiên có 2 chữ số mà chữ só hàng đơn vị gấp ba lần chữ số hàng chục là 39;26;13
ta lần lượt thử các số
viết ngược của 13 là 31, lớn hơn số ban đầu : 31-13=18 (loại)
viết ngược của 26 là 62, lớn hơn số ban đầu :62-26=36 (loại)
viết ngược của 39 là 93, lớn hơn số ban đầu :93-39=54 (thỏa mãn)
Vậy số cần tìm là 39
Gọi số cần tìm là \(ab\left(ab\in N.0< a< b< 10\right)\)
Ta có : \(b=3a\)
Khi đổi hai chữ số ta được số \(ba=10b+a\)
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình:
\(10b+a-54=10a+b\)
\(\Leftrightarrow9b-9a=54\)
\(\Leftrightarrow9.3a-9a=54\)
\(\Leftrightarrow18a=54\)
\(\Leftrightarrow a=3\left(tm\right)\)
Mà \(b=3a\) nên \(b=3\times3=9\left(tm\right)\)
Vậy số cần tìm là \(39\)
Gọi số cần tìm là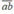 
= 10a + b (a, b ∈ N. 0 < a < b < 10)
Ta có b = 3a
Khi đổi hai chữ số ta được số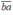 
= 10b + a
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình: 10b + a – 54 = 10a + b
⇔ 9b – 9a = 54
⇔ 9.3a – 9a = 54
⇔ 18a = 54
⇔ a =3 (tmđk)
Vậy số ban đầu cần tìm là 39.
Gọi chữ số hàng chục là x ( \(x\inℕ^∗\), \(4\le x\le9\))
Chữ số hàng đơn vị là: \(2x-7\)
Số tự nhiên ban đầu có dạng: \(10x+\left(2x-7\right)\)
Số tự nhiên ban đầu viết theo thứ tự ngược lại có dạng: \(10.\left(2x-7\right)+x\)
Nếu viết 2 chữ số ấy theo thứ tự ngược lại thì số mới nhỏ hơn số cũ 27 đơn vị nên ta có phương trình:
\(10.\left(2x-7\right)+x+27=10x+\left(2x-7\right)\)
\(\Leftrightarrow20x-70+x+27=10x+2x-7\)
\(\Leftrightarrow20x+x-10x-2x=-7+70-27\)
\(\Leftrightarrow9x=36\)\(\Leftrightarrow x=4\)( thoả mãn ĐK )
Vậy chữ số cần tìm là: \(41\)
Bài 1:
Gọi 2 số là a,b (\(a,b\inℤ\))
Ta có: a+b=51(*)
Mà 2/5a=1/6b
=> a=5/12b
Thay vào (*) ta có: 17/12b=51
=>b=36
Bài 1 :
Gọi số thứ nhất và số thứ hai lần lượt là x và y (x,y thuộc z)
Tổng hai số bằng : \(x+y=51\left(1\right)\)
Biết 2/5 số thứ nhất thì bằng 1/6 số thứ hai
\(x\frac{2}{5}-y\frac{1}{6}=0\left(2\right)\)
Từ 1 và 2 ta suy ra được hệ phương trình sau :
\(\hept{\begin{cases}x+y=51\\x\frac{2}{5}-y\frac{1}{6}=0\end{cases}}\)\(< =>\hept{\begin{cases}x=51-y\\\frac{2x}{5}-\frac{y}{6}=0\end{cases}}\)
\(< =>\frac{\left(51-y\right)2}{5}-\frac{y}{6}=0\)\(< =>\frac{102-2y}{5}-\frac{y}{6}=0\)
\(< =>\frac{102-2y}{5}=\frac{y}{6}\)\(< =>\left(102-2y\right)6=5y\)
\(< =>612-12y=5y\)\(< =>612=17y\)
\(< =>y=\frac{612}{17}=36\left(3\right)\)
Thay 3 vào 1 ta được : \(x+y=51\)
\(< =>x+36=51< =>x=51-36=15\)
Vậy số thứ nhất và số thứ hai lần lượt là 15 và 36
ab=62