Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
A=a^3-13a=a^3-a-12a
=a(a-1)(a+1)-12a
Vì a;a-1;a+1 là ba số liên tiếp
nên a(a-1)(a+1) chia hết cho 3!=6
mà 12a chia hết cho 6
nên A chia hết cho 6

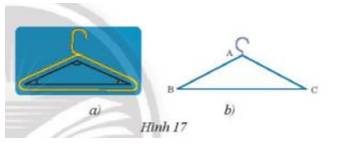
Vì tam giác ABC cân tại A
\( \Rightarrow \) AB = AC = 20 cm
\( \Rightarrow \) Chu vi tam giác ABC = AB + AC + BC = 20 + 20 + 28 = 68 cm
Vì \(\Delta ABC \) cân tại A \( \Rightarrow \widehat B = \widehat C\) = 35°
Mà tổng 3 góc trong một tam giác là 180°
\( \Rightarrow \widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {35^o} - {35^o} = {110^o}\)

a) Ta có: \(34^{2005}-34^{2004}\)
\(=17^{2005}\cdot2^{2005}-17^{2004}\cdot2^{2004}⋮17\)
b) Ta có: \(43^{2004}+43^{2005}\)
\(=43^{2004}\left(1+43\right)\)
\(=43^{2004}\cdot44⋮11\)
c) Ta có: \(27^3+9^5=3^9+3^{10}=3^9\left(1+3\right)=3^9\cdot4⋮4\)

Trừ mỗi vế cho 1, ta có:
\(\frac{b-16a+16c}{4a}=\frac{c-16b+16a}{4b}=\frac{a-16c+16b}{4c}=\frac{a+b+c}{4.\left(a+b+c\right)}=\frac{1}{4}\)(vì a,b,c > 0 nên a+b+c>0)
\(\Leftrightarrow\hept{\begin{cases}b+16c=17a\\c+16a=17b\\a+16b=17c\end{cases}}\Leftrightarrow a=b=c\)
tự thay vào

Hình hộp chữ nhật: Bể cá, viên gạch, tủ lạnh, máy giặt,…

Hình lập phương: Quân xúc xắc, viên đá, cái hộp,…

Ta có: \(\left(16a+17b\right)\left(17a+16b\right)⋮11\) Vì 11 là số nguyên tố
=> \(\orbr{\begin{cases}16a+17b⋮11\\17a+16b⋮11\end{cases}}\)
Không mất tính tổng quát. G/S: \(16a+17b⋮11\). (1)
Chúng ta chứng minh: \(17a+16b⋮11\)
Vì \(16a+17b⋮11\)
=> \(2\left(16a+17b\right)⋮11\)
=> \(32a+34b⋮11\)
=> \(\left(33a+33b\right)-\left(a-b\right)⋮11\)
Vì \(33a+33b=11\left(3a+3b\right)⋮11\)
=> \(\left(a-b\right)⋮11\)
=> \(\left(33a+33b\right)+\left(a-b\right)⋮11\)
=> \(34a+32b⋮11\)
=> \(2\left(17a+16b\right)⋮11\) mà 2 không chia hết cho 11
=> \(17a+16b⋮11\) (2)
Từ (1) và (2) => \(\left(17a+16b\right)\left(16a+17b\right)⋮\left(11.11\right)\)
=> \(\left(17a+16b\right)\left(16a+17b\right)⋮121\)
Cách khác:
Có: \(\left(16a+17b\right)\left(17a+16b\right)⋮11\) ( vì 11 là số nguyên tố)
=> \(\orbr{\begin{cases}16a+17b⋮11\\17a+16b⋮11\end{cases}}\)
G/s: \(16a+17b⋮11\)(1)
Mà \(\left(16a+17b\right)+\left(17a+16b\right)=\left(33a+33b\right)=11\left(3a+3b\right)⋮11\)
=> \(17a+16b⋮11\)(2)
Từ (1); (2) => \(\left(16a+17b\right)\left(17a+16b\right)⋮121\)