Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)0,6.a
b)\(a^2\).(a-3)
c)36.(a-1)
d)\(\dfrac{1.a^2}{a-b}\).(a-b)

a, \(2\sqrt{a^2}-5a=2\left|a\right|-5a\)do a < 0
\(=-2a-5a=-7a\)
b, \(\sqrt{25a^2}+3a=\sqrt{\left(5a\right)^2}+3a=\left|5a\right|+3a\)do \(a\le0\)
TH1 : \(-5a+3a=-2a\)với \(a< 0\)
hoặc TH2 : \(5+3=8\)
c, \(\sqrt{9a^4}+3a^2=\sqrt{\left(3a^2\right)^2}+3a^2=\left|3a^2\right|+3a^2\)
\(=3a^2+3a^2=6a^2\)do \(3>0;a^2\ge0\forall a\Rightarrow3a^2\ge0\forall a\)
d, \(5\sqrt{4a^6}-3a^3=5\sqrt{\left(2a^3\right)^2}-3a^3\)
\(=5\left|2a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)do \(a< 0\Rightarrow a^3< 0\)
a) \(2\sqrt{a^2}-5a\)=2\(|a|\)-5a = -2a-5a=-7a
b) \(\sqrt{25a^2}\) +3a = 5\(|a|\) + 3a=5a+3a=8a.
c) \(\sqrt{9a^4}\) + 3\(a^2\)=6\(a^2\)
d) \(5\sqrt{4a^6}\) - 3\(a^3\)=-13\(a^3\)

(Vì x > 0 nên |x| = x; y2 > 0 với mọi y ≠ 0)
(Vì x2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên |y3| = y3)
(Vì x2y4 = (xy2)2 > 0 với mọi x ≠ 0, y ≠ 0)

a/ \(\sqrt{\frac{2a}{3}}\cdot\sqrt{\frac{3a}{8}}\)
\(=\sqrt{\frac{2a}{3}\cdot\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\sqrt{\frac{a^2}{2^2}}=\sqrt{\left(\frac{a}{2}\right)^2}=\left|\frac{a}{2}\right|\)
mak ta có \(a\ge0\)
\(\Rightarrow\left|\frac{a}{2}\right|=\frac{a}{2}\)\(\Rightarrow\sqrt{\frac{2a}{3}}\cdot\sqrt{\frac{3a}{8}}=\frac{a}{2}\)
b/ \(\sqrt{13a}\cdot\sqrt{\frac{52}{a}}\)
\(=\sqrt{13a\cdot\frac{52}{a}}=\sqrt{\frac{13a\cdot52}{a}}=\sqrt{13\cdot52}=\sqrt{13\cdot13\cdot4}=\sqrt{13^2\cdot2^2}=\sqrt{\left(13\cdot2\right)^2}=13\cdot2=26\)
c/ \(\sqrt{5a}\cdot\sqrt{45}-3a\)
\(=\sqrt{5a\cdot45a}-3a=\sqrt{5a\cdot5a\cdot9}-3a\)
\(=\sqrt{5^2\cdot a^2\cdot3^2}-3a=\left|5\cdot a\cdot3\right|-3a\)
\(=15\left|a\right|-3a\)
Có \(a\ge0\Rightarrow\left|a\right|=a\)
\(\Rightarrow15\left|a\right|-3a=15a-3a=12a\)
\(\Rightarrow\sqrt{5a}\cdot\sqrt{45}-3a=12a\)
d/ \(\left(3-a\right)^2-\sqrt{0,2}\cdot\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{0,2\cdot180a^2}\)
\(=\left(3-a\right)^2-\sqrt{0,2\cdot9\cdot2\cdot10\cdot a^2}\)
\(=\left(3-a\right)^2-\sqrt{4\cdot9\cdot a^2}\)
\(=\left(3-a\right)^2-\sqrt{2^2\cdot3^2\cdot a^2}\)
\(=\left(3-a\right)^2-\left|2\cdot3\cdot a\right|\)
\(=\left(3-a\right)^2-6\left|a\right|=9-6a+a^2-6\left|a\right|\)
Chia làm 2 Trường Hợp:
+ TH1 : \(9-6a+a^2-6a=9-12a+a^2\left(a\ge0\right)\)
+ TH2 : \(9-6a+a^2-\left(-6a\right)=9+a^2\left(a< 0\right)\)

a) Ta có : Vì \(x\ge0\)và \(y\ge0\)nên \(x+y\ge0\)\(\Leftrightarrow\left|x+y\right|=x+y\)
\(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}\)
\(=\frac{2}{x^2-y^2}\sqrt{\frac{3}{2}.\left(x+y\right)^2}\)
\(=\frac{2}{x^2-y^2}.\sqrt{\frac{3}{2}}.\left|x+y\right|\)
\(=\frac{2}{\left(x-y\right)\left(x+y\right)}.\sqrt{\frac{3}{2}}.\left(x+y\right)\)
\(=\frac{2}{x-y}.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.2.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{\frac{2^2.3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{6}=\frac{\sqrt{6}}{x-y}\)
a, \(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}=\frac{2}{x^2-y^2}\frac{\sqrt{3}\left|x+y\right|}{\sqrt{2}}=\frac{2\sqrt{3}\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\sqrt{2}}\)
do \(x\ge0;y\ge0\)
\(=\frac{2\sqrt{3}}{\sqrt{2}\left(x-y\right)}=\frac{2\sqrt{6}}{2\left(x-y\right)}=\frac{\sqrt{6}}{x-y}\)

a: \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{4}+\sqrt{6}+\sqrt{8}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=1+\sqrt{2}\)
b: \(\sqrt{\dfrac{2a}{3}}\cdot\sqrt{\dfrac{3a}{8}}=\sqrt{\dfrac{6a^2}{24}}=\sqrt{\dfrac{a^2}{4}}=\dfrac{a}{2}\)
c: \(\sqrt{5a\cdot45a}-3a=-15a-3a=-18a\)

\(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(\sqrt{2}-1\right)}{2-1}=2\sqrt{2}-2+2-\sqrt{2}=\sqrt{2}\)
\(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\)
\(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
\(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}=\dfrac{\left(a-\sqrt{a}\right)\left(1+\sqrt{a}\right)}{1-a}=\dfrac{a+a\sqrt{a}-\sqrt{a}-a}{1-a}=\dfrac{\sqrt{a}\left(a-1\right)}{1-a}=-\sqrt{a}\)
\(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)

1) \(\sqrt{\frac{24}{3}}\cdot\sqrt{\frac{3a}{8}}=\sqrt{\frac{72a}{24}}=\sqrt{3a}\)
2) \(\sqrt{13a}\cdot\sqrt{\frac{52}{a}}=\sqrt{\frac{13a\cdot52}{a}}=\sqrt{676}=26\)
3) \(\sqrt{5a}\cdot\sqrt{45a}-3a=\sqrt{225a^2}-3a=15a-3a=12a\)
4) \(\left(3-a\right)^2-\sqrt{0,2}\cdot\sqrt{180a^2}=a^2-6a+9-\sqrt{36a^2}=a^2-6a+9-6a=a^2-12a+9\)

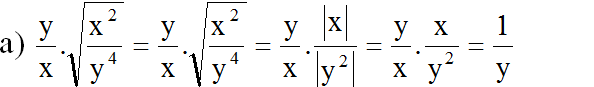
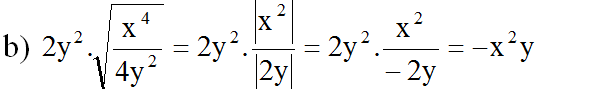
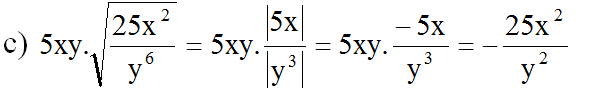
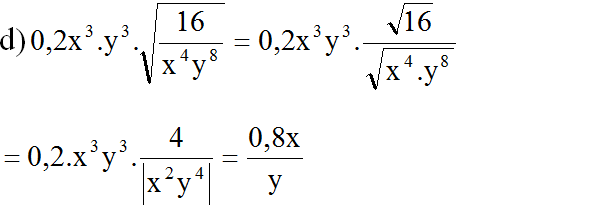

a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)
a) Ta có:
b) Ta có:
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:
d) Ta có: