Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1.
\(y'=6x^2+6\left(m-1\right)x+6\left(m-2\right)=6\left(x+1\right)\left(x+m-2\right)\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-m+2\end{matrix}\right.\)
Phương trình nghịch biến trên đoạn có độ dài lớn hơn 3 khi:
\(\left|-1-\left(-m+2\right)\right|>3\)
\(\Leftrightarrow\left|m-3\right|>3\Rightarrow\left[{}\begin{matrix}m>6\\m< 0\end{matrix}\right.\)
2.
\(y'=-3x^2+6x+m-1\)
\(\Delta'=9+3\left(m-1\right)>0\Rightarrow m>-2\)
Gọi \(x_1;x_2\) là 1 nghiệm của pt \(-3x^2+6x+m-1=0\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=\dfrac{-m+1}{3}\end{matrix}\right.\)
Hàm đồng biến trên đoạn có độ dài lớn hơn 1 khi:
\(\left|x_1-x_2\right|>1\)
\(\Leftrightarrow\left(x_1-x_2\right)^2>1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2>1\)
\(\Leftrightarrow4-\dfrac{-4m+4}{3}>1\)
\(\Rightarrow m>-\dfrac{5}{4}\) \(\Rightarrow m=-1\)
Có đúng 1 giá trị nguyên âm của m thỏa mãn
3.
\(y'=x^2+6\left(m-1\right)x+9\)
\(\Delta'=9\left(m-1\right)^2-9>0\Rightarrow\left[{}\begin{matrix}m>1\\m< 0\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-6\left(m-1\right)\\x_1x_2=9\end{matrix}\right.\)
\(\left|x_1-x_2\right|=6\sqrt{3}\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=108\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=108\)
\(\Leftrightarrow36\left(m-1\right)^2-36=108\)
\(\Rightarrow\left(m-1\right)^2=4\Rightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Có 1 giá trị nguyên âm của m thỏa mãn
8.
Hàm có 1 điểm cực đại \(\left(x=-1\right)\)
9.
Hàm có 1 điểm cực tiểu (\(x=-1\))
14.
\(y'=\dfrac{2x\left(x+1\right)-\left(x^2+3\right)}{\left(x+1\right)^2}=\dfrac{x^2+2x-3}{\left(x+1\right)^2}\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Xét dấu y' trên trục số:
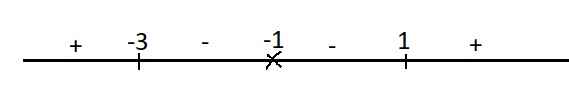
Từ dấu của y' ta thấy \(x=1\) là điểm cực tiểu
\(\Rightarrow y_{CT}=y\left(1\right)=2\)
31.
\(y'=\dfrac{1+m}{\left(x+1\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(\dfrac{1+m}{\left(x+1\right)^2}>0\Rightarrow m>-1\) (C)
32.
\(y'=\dfrac{4-m^2}{\left(x+4\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(4-m^2>0\Rightarrow-2< m< 2\)
\(\Rightarrow m=\left\{-1;0;1\right\}\)
Có 3 giá trị nguyên của m
33.
\(y'=\dfrac{m-1}{\left(x+1\right)^2}\)
Hàm đồng biến trên từng khoảng xác định khi:
\(m-1>0\Rightarrow m>1\)
34.
\(y'=\dfrac{2m-1}{\left(x+2m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}2m-1>0\\-2m>-3\end{matrix}\right.\) \(\Rightarrow\dfrac{1}{2}< m< \dfrac{3}{2}\)
\(\Rightarrow m=1\)
Có 1 giá trị nguyên của m
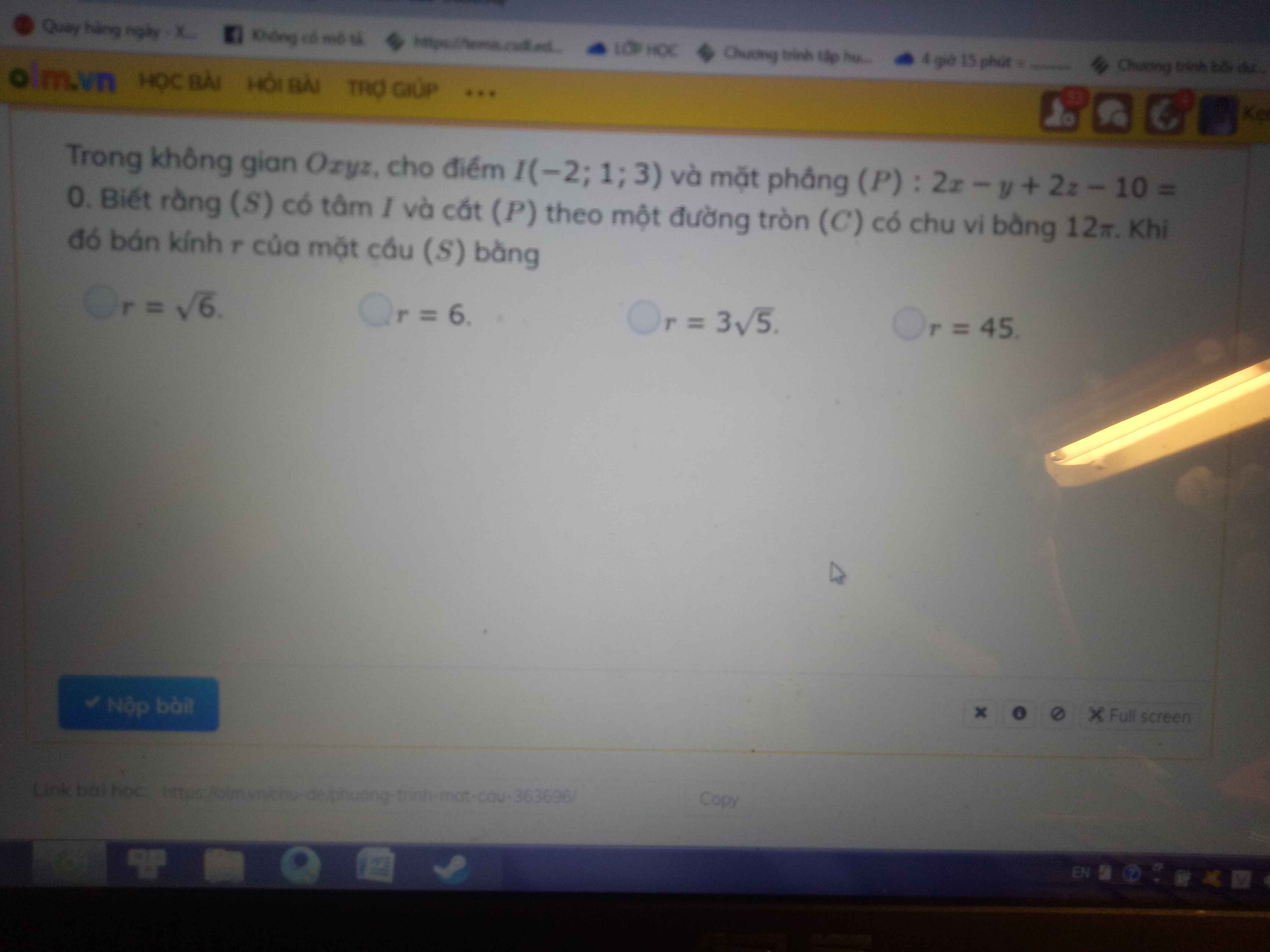
Gọi R là bán kính (C) \(\Rightarrow2\pi R=12\pi\Rightarrow R=6\)
Gọi \(J\) là tâm (C) \(\Rightarrow IJ\perp\left(P\right)\Rightarrow IJ=d\left(I;\left(P\right)\right)\)
\(d\left(I;\left(P\right)\right)=\dfrac{\left|2.\left(-2\right)-1.1+2.3-10\right|}{\sqrt{2^2+\left(-1\right)^2+2^2}}=3\)
\(\Rightarrow IJ=3\)
Áp dụng định lý Pitago:
\(r^2=IJ^2+R^2=45\Rightarrow r=3\sqrt{5}\)
Đường tròn (C)(C) có bán kính R = 6R=6.
d(I,(P))=3.
Mặt cầu (S) cắt mặt phẳng (P) theo một đường tròn
(C)(C) nên có bán kính:
r=\(\sqrt{R^2+(d(I,(P)))^2 } =3\sqrt{5}
\)(P(P) theo một đường tròn (C)(C) nên có bán kính:(S)(S) cắt mặt phẳng (P)
nhờ người ta giải mà cười hihi
em thì bó tay chấm chữ com vào ăn
TXĐ: D=R
\(9^{x^2+x-1}-10.3^{x^2+x-2}+1=0\)
\(\Leftrightarrow9^{x^2+x-1}-10.\frac{3^{x^2+x-1}}{3}+1=0\)
Đặt t = \(3^{x^2+x-1}\) (t>0)
\(\Leftrightarrow t^2-\frac{10}{3}t+1=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}t=3\\t=\frac{1}{3}\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}3^{x^2+x-1}=3\\3^{x^2+x-1}=\frac{1}{3}\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2+x-1=1\\x^2+x-1=\frac{1}{3}\end{array}\right.\)
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ
Mình nghĩ câu nói này của Bác mang ý nghĩa: Làm việc gì cũng phải chắc chắn, có lý luận, có hiểu biết thì ta mới giải được vấn đề.
Đúng k mình nha
#Hoctot
“Lý luận như cái kim chỉ nam, nó chỉ phương hướng cho chúng ta trong công việc thực tế.
Không có lý luận thì lúng túng như nhắm mắt mà đi…
Có kinh nghiệm mà không có lý luận, cũng như một mắt sáng, một mắt mờ…
Lý luận mà không áp dụng vào thực tế là lý luận suông”.
Vai trò quan trọng như vậy, nhưng “kém lý luận” vẫn là căn bệnh đang tồn tại ở một bộ phận không nhỏ cán bộ, đảng viên.
bạn chỉ cần tách x4-1 thành (x2-1)(x2+1),rồi đặt x2=t là ok
Lời giải:
\(\lim\limits_{x\to 2-}y=\lim\limits_{x\to 2-}\frac{\sqrt{4-x^2}}{(x-2)(x-3)}=\lim\limits_{x\to 2-}\frac{\sqrt{2+x}}{\sqrt{2-x}(x-3)}=-\infty \) nên $x=2$ là TCĐ
Vì \(x\in [-2;2)\) nên không tồn tại \(\lim\limits_{x\to +\infty }y\) nên đths không có TCN
Còn $x=3$ không thể là TCĐ vì tại $x=3$ thì $\sqrt{4-x^2}$ không tồn tại .
Đáp án A