Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

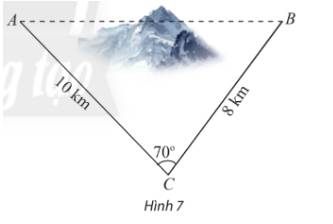
Để lắp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi. Do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 10 km rồi nối từ vị trí C đến vị trí B dài 8 km biết góc tạo bởi hai đoạn dây AC và BC là 75 độ. Hỏi so với việc nối thẳng từ A đến B phải tốn hết bao nhiêu mét dây?

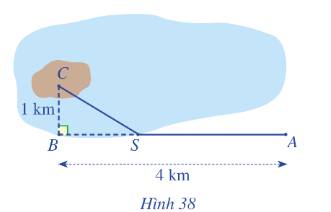
Gọi khoảng cách từ A đến S là x (km) (0<x<4)
\( \Rightarrow BS = 4 - x\)(km)
\( \Rightarrow CS = \sqrt {C{B^2} + B{S^2}} \)\( = \sqrt {1 + \left( {4 - {x^2}} \right)} \)(km)
Tổng số tiền từ A đến C là:
\(3.SA + 5.SC = 3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} \)(triệu đồng)
Khi đó ta có phương trình:
\(3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16\)
\( \Leftrightarrow 5\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16 - 3x\)
\(\begin{array}{l}25.\left( {{x^2} - 8x + 17} \right) = {\left( {16 - 3x} \right)^2}\\ \Leftrightarrow 25{x^2} - 200x + 425 = 256 - 96x + 9{x^2}\\ \Leftrightarrow 16{x^2} - 104x + 169 = 0\\ \Leftrightarrow x = \frac{{13}}{4}\left( {tm} \right)\end{array}\)
Do \(16 - 3x > 0 \Leftrightarrow \forall 0 < x < 4\)
=> \(SC = \sqrt {1 + \left( {4 - {x^2}} \right)} = 1,25\)
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)

Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
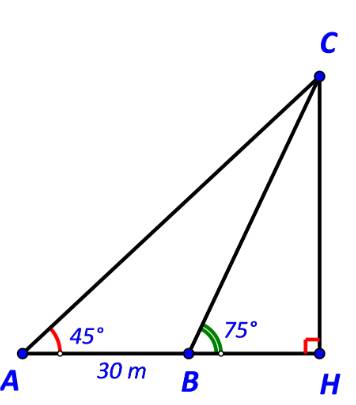
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.

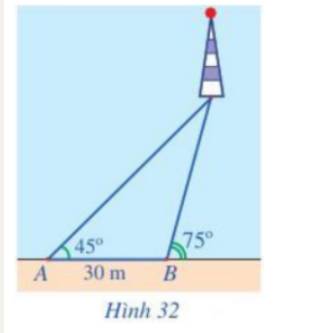
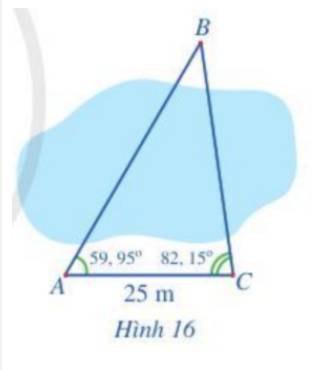
Xét tam giác ABC, ta có: \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\)
\( \Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}\)
Áp dụng định lí sin trong tam giác BAC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin {37,9^o}}} \approx 40\)
Vậy khoảng cách từ vị trí A đến vị trí B là 40 m.

Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.

Bình phương hai vế ta được:
\(\begin{array}{l}{(8 - 40x)^2} + {(7 - 40x)^2} = 25\\ \Leftrightarrow 64 - 640x + 1600{x^2} + 49 - 560x + 1600{x^2} = 25\\ \Leftrightarrow 3200{x^2} - 1200x + 88 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11}}{{40}}\\x = \frac{1}{{10}}\end{array} \right.\end{array}\)
Vậy phương trình có hai nghiệm là \(x = \frac{{11}}{{40}}\) và \(x = \frac{1}{{10}}\).



Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\\ \Leftrightarrow A{B^2} = {8^2} + {10^2} - 2.8.10.\cos {70^o}\\ \Rightarrow AB \approx 10,45\end{array}\)
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
\(AC + CB - AB = 10 + 8 - 10,45 = 7,55\;(km).\)