
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
π(2R)2 = 4πR2
π(3R)2 = 9 πR2
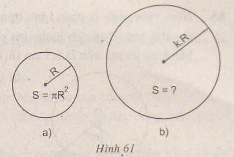
π(kR)2 = k2 πR2
Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với k > 0 thì diện tích hình tròn sẽ gấp k2 lần
Ta có:
π(2R)2 = 4πR2
π(3R)2 = 9 πR2
π(kR)2 = k2 πR2
Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với k > 0 thì diện tích hình tròn sẽ gấp k2 lần.

Giải
.png)
a) Ta có: OM⊥JM (JM là tiếp tuyến của (O))
NK⊥JM (K là trực tâm của ΔJMN)
⇒ OM // NK
Chứng minh tương tự được ON // MK
⇒ OMKN là hình bình hành
Hình bình hành OMKN có hai đường chéo OK và MN cắt nhau tại H
=⇒ H là trung điểm của OK.
b) Hình bình hành OMKN có OM = ON = a nên là hình thoi
⇒ OM = MK ⇒ΔOMK cân tại M
ΔOMJ vuông tại M, có:
có \(\widehat{MOJ}=\frac{OM}{OJ}=\frac{a}{2a}=\frac{1}{2}\Rightarrow\widehat{MOJ}=60^0\)
⇒ΔOMK là tam giác đều
⇒OK = OM = a ⇒K ∈ (O ; a)
c) ΔOMH vuông tại H
⇒MH = OM . sin\(\widehat{MOH}\)=a . sin\(60^0=\frac{a\sqrt{3}}{2}\)hay \(\frac{a\sqrt{3}}{2}\)
Hok Tốt !
# mui #
Chú Thích : Mk có gửi ảnh nếu bn ko thấy thì vào thống kê hỏi đáp của mk nha

Mỉnh ko hiểu đề cho lắm. Tam giác ABC vuông tại A => AB vuông góc AC, vậy đề còn cho "Từ A vẽ đường vuông góc với AB và AC tại D và E" là sao??? Hơi vô lý.


không
trên mạng đầy.