Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left(\sqrt{x+2022}-\sqrt{y+2022}\right)+\left(x^3-y^3\right)=0\)
=>\(\dfrac{x-y}{\sqrt{x+2022}+\sqrt{y+2022}}+\left(x-y\right)\left(x^2+xy+y^2\right)=0\)
=>x-y=0
=>x=y
P=2x^2-5x^2+x^2+12x+2023
=-2x^2+12x+2023
=-2(x^2-6x-2023/2)
=-2(x^2-6x+9-2041/2)
=-2(x-3)^2+2041<=2041
Dấu = xảy ra khi x=3


1:
a: \(M=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)=x-y\)
b: M=N
=>x-y=2 căn x-y+15
=>x-2căn x-15=0
=>x=25
2:
a: Khi m=0 thì pt sẽ là:
x^2-4x+3=0
=>x=1 hoặc x=3

1:
a: \(M=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)=x-y\)
b: M=N
=>x-y=2 căn x-y+15
=>x-2căn x-15=0
=>x=25
2:
a: Khi m=0 thì pt sẽ là:
x^2-4x+3=0
=>x=1 hoặc x=3

Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức. Trước tiên, ta mở đuôi công thức:(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)Từ phép nhân đầu tiên, ta có:(x+y)(x+y) = x^2 + 2xy + y^2Tiếp tục nhân với (x+y), ta có:(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3Lặp lại quá trình này 2020 lần nữa, ta có:(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4Tiếp tục nhân với (x+y), ta có:(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
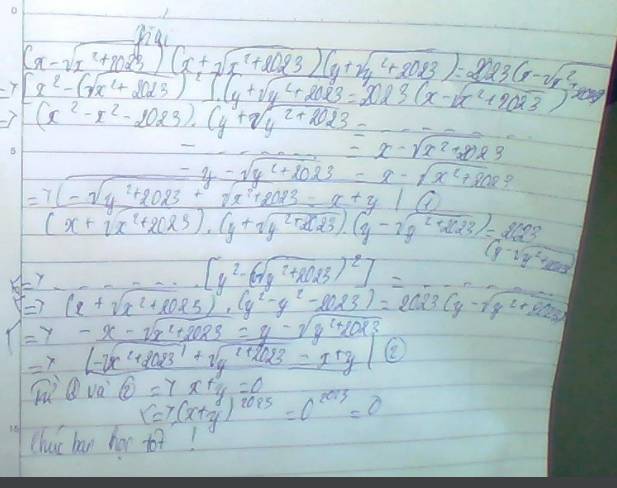
Lời giải:
\(A=2.2022^{2023}+2(1^{2023}+2^{2023}+3^{2023}+...+1010^{2023}+1011^{2023}+1012^{2023}+...+2021^{2023})\)
\(=2.2022^{2023}+2[(1^{2023}+2021^{2023})+(2^{2023}+2019^{2023})+...+(1010^{2023}+1012^{2023})+1011^{2023}]\)
\(=2.2022^{2023}+2.1011^{2023}+2[(1^{2023}+2021^{2023})+(2^{2023}+2019^{2023})+...+(1010^{2023}+1012^{2023})]\)
Dễ thấy: $2.2022^{2023}\vdots 2022; 2.1011^{2023}=2022.1011^{2023}\vdots 2022$
Đối với biểu thức trong ngoặc vuông thì: Nhớ rằng với mọi $n$ lẻ thì $a^n+b^n\vdots a+b$ nên $1^{2023}+2021^{2023}\vdots 2022; 2^{2023}+2019^{2023}\vdots 2022;...; 1010^{2023}+1012^{2023}\vdots 2022$
$\Rightarrow 2[(1^{2023}+2021^{2023})+(2^{2023}+2019^{2023})+....+(1010^{2023}+1012^{2023})]\vdots 2022$
Do đó $A\vdots 2022$