Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng.
Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.
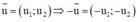
b) Sai.
Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.
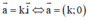
c) Đúng.
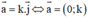

Lời giải:
Giả sử 3 vecto trên đôi một ngược hướng nhau
\(\overrightarrow{a}, \overrightarrow{b}\) ngược hướng
$\overrightarrow{c},\overrightarrow{b}$ ngược hướng
$\Rightarrow \overrightarrow{a}, \overrightarrow{c}$ cùng ngược hướng với $\overrightarrow{b}$
$\Rightarrow \overrightarrow{a}, \overrightarrow{c}$ cùng hướng (trái giả sử)
Vậy ít nhất 2 trong số 3 vecto cùng hướng.

Câu 1:
Đáp án A. Vecto $\overrightarrow{0}$ là vecto duy nhất cùng phương với mọi vecto.
Câu 2:
Đáp án C. Hai vecto bằng nhau thì cùng hướng chứ không chỉ đơn thuần có giá trùng/ song song với nhau.

a) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) có cùng độ dài bằng \(\left| {kt} \right|.\left| {\overrightarrow u } \right|\)
Ta có: \(\left| {t\overrightarrow u } \right| = \left| t \right|\left| {\overrightarrow u } \right| \Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| k \right|\left| {\left( {t\overrightarrow u } \right)} \right| = \left| k \right|.\left| t \right|\left| {\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
Và \(\left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
\( \Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
b) Nếu \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)
Ta xét 2 trường hợp:
Trường hợp 1: \(k \ge 0,t \ge 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(t\overrightarrow u \) (vì \(k \ge 0\) ), mà vecto \(t\overrightarrow u \) cùng hướng với vecto \(\overrightarrow u \) (vì \(t \ge 0\) )
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(\overrightarrow u \).
Trường hợp 2: \(k < 0,t < 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(t\overrightarrow u \) (vì \(k < 0\) ), mà vecto \(t\overrightarrow u \) ngược hướng với vecto \(\overrightarrow u \) (vì \(t < 0\) )
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(\overrightarrow u \).
Vậy vecto \(k\left( {t\overrightarrow u } \right)\) luôn cùng hướng với vecto \(\overrightarrow u \) nếu \(kt \ge 0\).
Lại có: \(kt \ge 0\) nên \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)
Vậy \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)
c) Nếu \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)
Ta xét 2 trường hợp:
Trường hợp 1: \(k > 0,t < 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(t\overrightarrow u \) (vì \(k > 0\) ), mà vecto \(t\overrightarrow u \) ngược hướng với vecto \(\overrightarrow u \) (vì \(t < 0\))
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(\overrightarrow u \).
Trường hợp 2: \(k < 0,t > 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(t\overrightarrow u \) (vì \(k < 0\) ), mà vecto \(t\overrightarrow u \) cùng hướng với vecto \(\overrightarrow u \) (vì \(t > 0\))
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(\overrightarrow u \).
Vậy vecto \(k\left( {t\overrightarrow u } \right)\) luôn ngược hướng với vecto \(\overrightarrow u \) nếu \(kt < 0\).
Lại có: \(kt < 0\) nên \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)
Vậy \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)
d)
Từ ý b) và c), ra suy ra hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \)luôn cùng hướng.
Theo câu a) ta có: \(\left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
\( \Rightarrow \) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) bằng nhau