Cho x,y >0Tìm mina) A= (x+9)(y+9)(1/x + 1/y)b) B= (1+xy)(1/x + 1/y)

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

MH

Minh Hiếu

10 tháng 8 2021

Cho x,y >0

Tìm min

a) A= (x+9)(y+9)(1/x + 1/y)

b) B= (1+xy)(1/x + 1/y)

2

TC

Trên con đường thành công không có....

10 tháng 8 2021

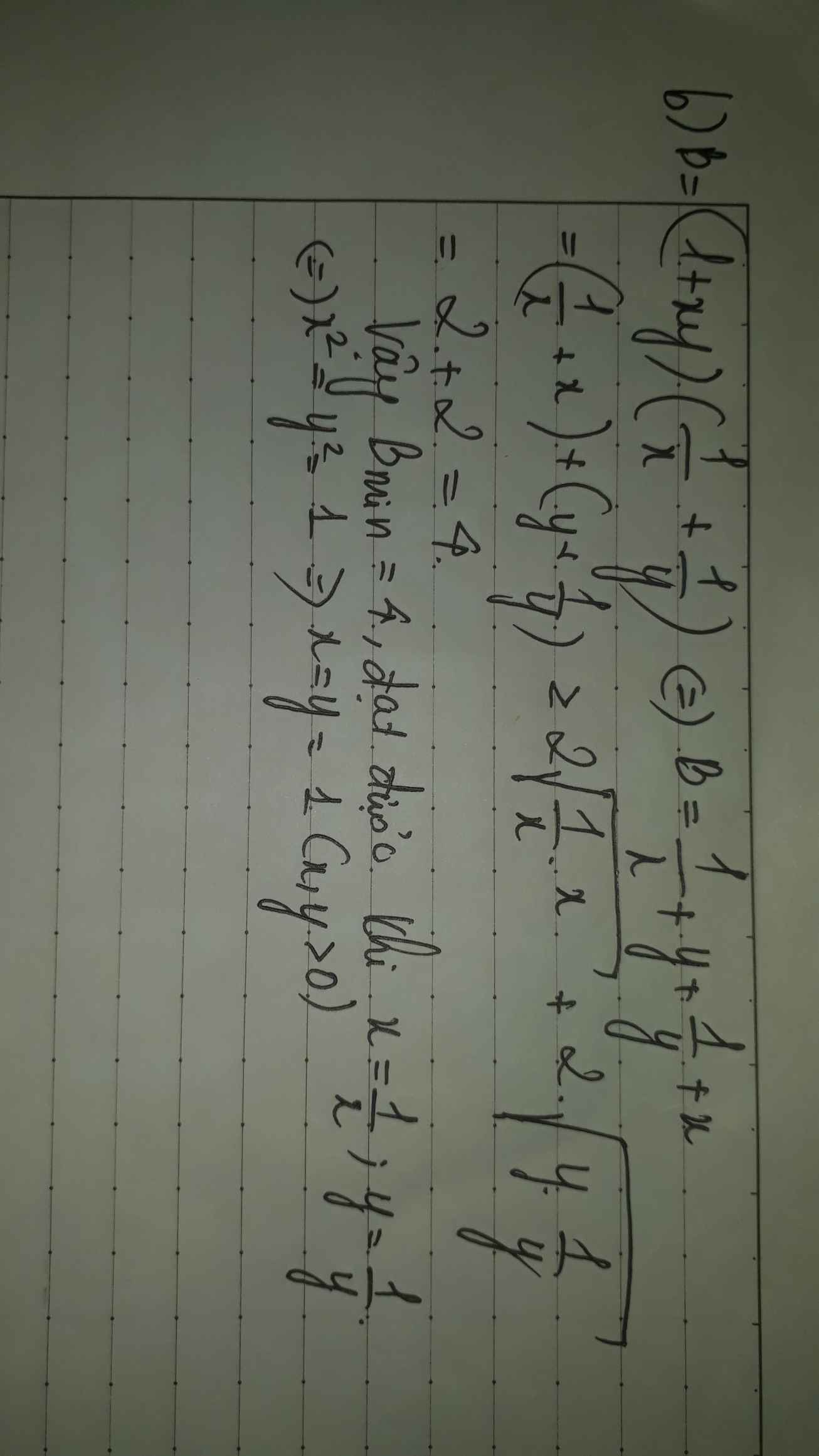
undefined

TC

Trên con đường thành công không có....

10 tháng 8 2021

undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

TP

thành piccolo

4 tháng 8 2015 - olm

a,cho x+y>=6;x,y>0,tìm min của p=5x+3y+10/x+8/y
b, a;b;c là 3 số thực dương thoả mãn a+2b+3c>=20. Tìm min của a+b+c+3/a+9/b+4/c
c,Cho x;y>0 thoả mãn x+y<=1, tìm min A=(1-1/x)-(1/y^2)
d,Cho a;b;c >0, a+b+c=<3/2, tìm min của A=a+b+c+1/a+1/b+1/c
e, Cho a,b dương,a;b=<1, tìm min của P=1/(a^2+b^2) +1/ab
g,Cho a;b;c>0, a+b+c=<1, tìm min của P=a+b+c+2(1/a+1/b+1/c)

1

ML

Mr Lazy

4 tháng 8 2015

Dự đoán dấu "=" và chọn điểm rơi phù hợp để áp dụng bất đẳng thức Trung bình cộng - Trung bình nhân

PT

Phạm Trần Hương Giang

26 tháng 9 2017 - olm

toàn bộ dùng bất đẳng thức svac-xơ hoặc bunhiacopskibài 1: cho x,y,z>0. CMR:a,1/x+1/y>=4/x+yb,1/x+1/y+1/z>=9/x+y+zbài 2: cho a,b,c>0. CMR:a,a^2/(b+c)+b^2/(c+a)+c^2/(a+b)>=(a+b+c)/2b, a^2/(2b+5c)+b^2/(2c+5a)+c^2/(2a+5b)>=(a+b+c)/7bài 3: cho a,b,c>0. CMR a/(b+c)+b/(c+a)+c/(b+a)>=3/2bài 4: cho a,b,c>0. CMR:1/(b+2c)+b/(c+2a)+c/(a+2b)>=1bài 5: cho a+b+c=1. Tìm mina, P=1/a+4/b+9/cb, Q+a^2/(b+3c)+b^2/(c+3a)+c^2/(a+3b)bài 6: cho 3x^2+5y^2=3/79tìm max, min A=x+4ybài 7: tìm min...

0

TS

Trần Sỹ Hội

25 tháng 7 2018 - olm

Câu 1: x>0,Tìm min A = \(3x^2\)+\(\frac{2}{x^3}\)

Câu 2: x,y>0 Tìm min S = \(\frac{x^2+y^2}{xy}+\frac{xy}{x^2+y^2}\)

Câu 3: \(\hept{\begin{cases}a,b,c>0\\a+b+c=1\end{cases}}\) Tìm min P \(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)

0

LT

Lê Thúy Ngà

20 tháng 6 2021 - olm

So sánh các số saua)\(A=2018.2020+2019.2021\) Và \(B=2019^2+2020^2-2\)b)\(A=10\left(9^2+1\right)\left(9^4+1\right)\left(9^8+1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)\)và\(B=9^{64}-1\)c)\(A=\frac{x-y}{x+y}\)và\(B=\frac{x^2-y^2}{x^2+xy+y^2}\)với x>y>0d)\(A=\frac{\left(x+y\right)^3}{x^2-y^2}\)và\(B=\frac{x^2-xy+y^2}{x-y}\)với...

2

XO

Xyz OLM

20 tháng 6 2021

Ta có A = 2018.2020 + 2019.2021

= (2020 - 2).2020 + 2019.(2019 + 2)

= 2020² - 2.2020 + 2019² + 2.2019

= 2020² + 2019² - 2(2020 - 2019) = 2020² + 2019² - 2 = B

=> A = B

b) Ta có B = 9⁶⁴ - 1= (9³²)² - 1²

= (9³² + 1)(9³² - 1) = (9³² + 1)(9¹⁶ + 1)(9¹⁶ - 1) = (9³² + 1)(9¹⁶ + 1)(9⁸ + 1)(9⁸ - 1)

= (9³² + 1)(9¹⁶ + 1)(9⁸ + 1)(9⁴ + 1)(9⁴ - 1)

= (9³² + 1)(9¹⁶ + 1)(9⁸ + 1)(9⁴ + 1)(9² + 1)(9² - 1)

(9³² + 1)(9¹⁶ + 1)(9⁸ + 1)(9⁴ + 1)(9² + 1).80

mà A = (9³² + 1)(9¹⁶ + 1)(9⁸ + 1)(9⁴ + 1)(9² + 1).10

=> A < B

XO

Xyz OLM

20 tháng 6 2021

c) Ta có A = \(\frac{x-y}{x+y}=\frac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right)^2}=\frac{x^2-y^2}{x^2+2xy+y^2}< \frac{x^2-y^2}{x^2+xy+y^2}=B\)

=> A < B

d) \(A=\frac{\left(x+y\right)^3}{x^2-y^2}=\frac{\left(x+y\right)^3}{\left(x+y\right)\left(x-y\right)}=\frac{\left(x+y\right)^2}{x-y}=\frac{x^2+2xy+y^2}{x-y}< \frac{x^2-xy+y^2}{x-y}=B\)

=> A < B

LT

Lê Thảo Vy

20 tháng 10 2017 - olm

cho x,y>0 x+y=0 tìm MIN

A=\(\frac{1}{x^2+y^2}\)\(+\frac{1}{xy}\)

1

NN

Nguyễn Ngọc Tuấn Anh

1 tháng 11 2019

Sao đã có x,y>0 lại có x+y=0 vậy bạn

ND

Nguyễn Dũng

21 tháng 7 2018

So sánh

a, 2011.2013+2012.2014 và 2012^2+2013^2-2

b, (9-1)(9^2+1)(9^4+1)(9^8+1)(9^16+1)(9^32+1) và 9^64-1

c, x-y/x+y và x^2-y^2/x^2+xy+y^2 với x>y>0

Giúp mình nha!!!

2

Y

Yukru

23 tháng 7 2018

a) \(2011.2013+2012.2014\)

\(=\left(2012-1\right)\left(2012+1\right)+\left(2013-1\right)\left(2013+1\right)\)

\(=2012^2-1+2013^2-1\)

\(=2012^2+2013^2-2\)

\(\Rightarrow2011.2013+2012.2014=2012^2+2013^2-2\)

b) \(\left(9-1\right)\left(9^2+1\right)\left(9^4+1\right)\left(9^8+1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)\)

\(=\dfrac{1}{10}\left(9+1\right)\left(9-1\right)\left(9^2+1\right)\left(9^4+1\right)\left(9^8+1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)\)

\(=\dfrac{1}{10}\left(9^2-1\right)\left(9^2+1\right)\left(9^4+1\right)\left(9^8+1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)\)

\(=\dfrac{1}{10}\left(9^4-1\right)\left(9^4+1\right)\left(9^8+1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)\)

\(=\dfrac{1}{10}\left(9^8-1\right)\left(9^8+1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)\)

\(=\dfrac{1}{10}\left(9^{16}-1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)\)

\(=\dfrac{1}{10}\left(9^{32}-1\right)\left(9^{32}+1\right)\)

\(=\dfrac{1}{10}\left(9^{64}-1\right)\)

\(=\dfrac{9^{64}-1}{10}\)

Ta có: \(9^{64}-1=\dfrac{10\left(9^{64}-1\right)}{10}\)

Mà \(\dfrac{10\left(9^{64}-1\right)}{10}>\dfrac{9^{64}-1}{10}\)

\(\Rightarrow\left(9-1\right)\left(9^2+1\right)\left(9^4+1\right)\left(9^8+1\right)\left(9^{16}+1\right)\left(9^{32}+1\right)< 9^{64}-1\)

c) Ta có:

\(\dfrac{x^2-y^2}{x^2+xy+y^2}=\dfrac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right)^2-xy}\left(1\right)\)

Vì x>y>0, ta có:

\(\dfrac{x-y}{x+y}=\dfrac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right)^2}\left(2\right)\)

Vì x>y>0 nên \(\left(x+y\right)^2-xy< \left(x+y\right)^2\left(3\right)\)

Từ (1), (2) và (3) suy ra:

\(\dfrac{x-y}{x+y}< \dfrac{x^2-y^2}{x^2+xy+y^2}\)

PT

Phong Thần

18 tháng 9 2018

a) Ta có:

\(2011.2013+2012.2014\)

\(=\left(2012-1\right)\left(2012+1\right)+\left(2013-1\right)\left(2013+1\right)\)

\(=2012^2-1+2013^2-1\)

\(=2012^2+2013^2-2\)

Vậy 2011.2013+2012.2014 = 2012² + 2013² - 2

GV

Giap van Khoi

23 tháng 8 2017 - olm

1/ Chung to

a/ a^2+b^2+1+2ab>0

b/x^2-x+1>0

2/Phan tich

a/x(y-1)+y(1-y)

b/10x(x-y)-8y(y-x)

c/x^2+6x -y^2+9

d/x^2+5x+4

e/x^2-xy+x-y

f/3x^2-3xy-5x-5y

g/xz+yz-5(x+y)

1

B

Bexiu

23 tháng 8 2017

Bài làm

a) x⁴+x³+2x²+x+1=(x⁴+x³+x²)+(x²+x+1)=x²(x²+x+1)+(x²+x+1)=(x²+x+1)(x²+1)

b)a³+b³+c³-3abc=a³+3ab(a+b)+b³+c³ -(3ab(a+b)+3abc)=(a+b)³+c³-3ab(a+b+c)

=(a+b+c)((a+b)²-(a+b)c+c²)-3ab(a+b+c)=(a+b+c)(a²+2ab+b²-ac-ab+c²-3ab)=(a+b+c)(a²+b²+c²-ab-ac-bc)

c)Đặt x-y=a;y-z=b;z-x=c

a+b+c=x-y-z+z-x=o

đưa về như bài b

d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung

e)x²(y-z)+y²(z-x)+z²(x-y)=x²(y-z)-y²((y-z)+(x-y))+z²(x-y)

=x²(y-z)-y²(y-z)-y²(x-y)+z²(x-y)=(y-z)(x²-y²)-(x-y)(y²-z²)=(y-z)(x²-2y²+xy+xz+yz)

TL

Trọng Lễ

8 tháng 12 2016 - olm

1) cho x>0,y>0 thỏa mãn x+y=1.tìm GTNN của biểu thức P= 1/xy+2/x^2+y^2

2)cho x>0,y>0 và x+y=1.tìm GTNN của M=3/xy+2/x^2+y^2

3)tìm GTNN và GTLN của

N= 2x+1/x^2+2

Q= 2x^2-2x+9/x^2+2x+5

R=2(x^2+x+1)/x^2+1

0

PT

Phạm Trần Hương Giang

30 tháng 9 2017

toàn bộ dùng bất đẳng thức svac-xơ hoặc bunhiacopski bài 1: cho x,y,z>0. CMR: a,1/x+1/y>=4/x+y b,1/x+1/y+1/z>=9/x+y+z bài 2: cho a,b,c>0. CMR: a,a^2/(b+c)+b^2/(c+a)+c^2/(a+b)>=(a+b+c)/2 b, a^2/(2b+5c)+b^2/(2c+5a)+c^2/(2a+5b)>=(a+b+c)/7 bài 3: cho a,b,c>0. CMR a/(b+c)+b/(c+a)+c/(b+a)>=3/2 bài 4: cho a,b,c>0. CMR: 1/(b+2c)+b/(c+2a)+c/(a+2b)>=1 bài 5: cho a+b+c=1. Tìm min a, P=1/a+4/b+9/c b, Q+a^2/(b+3c)+b^2/(c+3a)+c^2/(a+3b) bài 6: cho 3x^2+5y^2=3/79 tìm max,...

0

BV

Bảy việt Nguyễn

25 tháng 6 2017 - olm

1. cho x^2+y^2=1. tìm Min Max x+y

2. cho xy=1 x>y. tìm min (x^2+y^2)/(x-y)

0