Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)

Ta có:
\(\left. \begin{array}{l}\left( {ABD} \right) \bot \left( {BCD} \right)\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\C{\rm{D}} \subset \left( {BCD} \right)\\C{\rm{D}} \bot B{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABD} \right) \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)
Vậy tam giác \(ACD\) vuông tại \(D\).

tham khảo:

a) Vì SA⊥(ABCD) nên SA⊥CD
Ta có: DC⊥AD;DC⊥SA nên DC⊥(SAD)
b) Vì SA⊥(ABCD) nên SA⊥CM
Ta có: AB = 2CD nên AM = CD. Suy ra AMCD là hình chữ nhật nên CM⊥AB
Mà CM⊥SA
Suy ra: CM⊥(SAB)

tham khảo:

a) Tam giác ABD có HK là đường trung bình nên HK//BD
Vì ABCD là hình vuông nên AC⊥BD. Suy ra AC⊥HK
Vì SH⊥(ABCD) nên SH⊥AC
Ta có: AC⊥SH,AC⊥HK nên AC⊥(SHK)
b) Ta có tam giác AHD và tam giác DKC bằng nhau nên DH⊥CK
Mà SH⊥(ABCD) nên SH⊥CK
Suy ra CK⊥(SDH)

\(\begin{array}{l}\left. \begin{array}{l} + )AC \bot BD\,\,\left( {hv\,\,ABCD} \right)\\SA \bot BD\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} + )BD \bot SC\left( {BD \bot \left( {SAC} \right)} \right)\\BM \bot SC\\BD \cap BM = \left\{ B \right\}\end{array} \right\} \Rightarrow SC \bot \left( {MBD} \right)\end{array}\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
\(\left. \begin{array}{l}SC \bot \left( {MBD} \right)\\OM \subset \left( {MBD} \right)\end{array} \right\} \Rightarrow SC \bot OM\)
Mà \(AH \bot SC\)
\( \Rightarrow AH//OM,OM \subset \left( {MBD} \right) \Rightarrow AH//\left( {MBD} \right)\)

tham khảo:

a) Tam giác SAB có MN là đường trung bình nên MN//SA
Mà SA⊥(ABCD) nên MN⊥(ABCD). Suy ra MN⊥AB
Hình thang ABCD có NP là đường trung bình nên NP//BC//AD. Mà BC⊥AB nên NP⊥ABTa có AB vuông góc với hai đường thẳng MN và NP cắt nhau cùng thuộc (MNPQ) nên AB⊥(MNPQ)
b) Vì AB⊥(MNPQ);MQ∈(MNPQ) nên AB⊥MQ
Tam giác SBC có MQ là đường trung bình nên MQ//BC. Mà SA⊥BC nên SA⊥MQ
Ta có MQ vuông góc với hai đường thẳng SA và AB cắt nhau cùng thuộc (SAB) nên MQ⊥(SAB)

.png)
\(\begin{array}{l}\left. \begin{array}{l} + )BC \bot AB\left( {hcn\,\,ABCD} \right)\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AB \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right);AM \subset \left( {SAB} \right) \Rightarrow BC \bot AM\\\left. \begin{array}{l} + )CD \bot AD\left( {hcn\,\,ABCD} \right)\\CD \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AD \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right);AN \subset \left( {SAD} \right) \Rightarrow CD \bot AN\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l} + )AM \bot SB\\AM \bot BC\\SB \cap BC = \left\{ B \right\}\end{array} \right\} \Rightarrow AM \bot \left( {SBC} \right);SC \subset \left( {SBC} \right) \Rightarrow SC \bot AM\\\left. \begin{array}{l} + )AN \bot SD\\AN \bot CD\\SD \cap CD = \left\{ D \right\}\end{array} \right\} \Rightarrow AN \bot \left( {SCD} \right);SC \subset \left( {SCD} \right) \Rightarrow SC \bot AN\\\left. \begin{array}{l} + )AM \bot SC\\AN \bot SC\\AM \cap AN = \left\{ A \right\}\end{array} \right\} \Rightarrow SC \bot \left( {AMN} \right)\end{array}\)

A B C D N S M P H K
a) (SAB) và (SAD) cùng vuông góc (ABCD), (SAB) và (SAB) có giao tuyến SA => SA vuông góc (ABCD)
=> BC vuông góc SA. Mà BC vuông góc AB nên BC vuông góc (SAB).
Ta cũng có BD vuông góc AS, BD vuông góc AC vì ABCD là hình vuông
=> BD vuông góc (SAC) hay (SAC) vuông góc (SBD).
b) Gọi M là trung điểm của AB, CM cắt AD tại P, H thuộc CM sao cho AH vuông góc CM, K thuộc SH sao cho AK vuông góc SH.
Dễ thấy AN || CM => AN || (SCM) => d(AN,SC) = d(AN,SCM) = d(A,SCM) = d(A,SMP)
Ta có AH vuông góc MP, MP vuông góc AS => MP vuông góc (HAS) => (SMP) vuông góc (HAS)
Vì (SMP) và (HAS) có giao tuyến SH, AK vuông góc SH tại K nên d(A,SMP) = AK
Theo hệ thức lượng thì: \(\frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AM^2}+\frac{1}{AP^2}\)
\(\Rightarrow d\left(AN,SC\right)=d\left(A,SMP\right)=AK=\frac{AS.AM.AP}{\sqrt{AS^2AM^2+AM^2AP^2+AP^2AS^2}}\)
\(=\frac{a\sqrt{2}.\frac{a}{2}.a}{\sqrt{2a^2.\frac{a^2}{4}+\frac{a^2}{4}.a^2+a^2.2a^2}}=\frac{a\sqrt{22}}{11}.\)
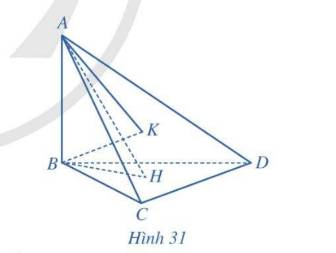

a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\)
Mà \(CD \bot BC\)\( \Rightarrow CD \bot \left( {ABC} \right)\)
Lại có \(BM \in \left( {ABC} \right)\)\( \Rightarrow CD \bot BM\)
b) Ta có \(\left. \begin{array}{l}BM \bot CD\\BM \bot AC\end{array} \right\} \Rightarrow BM \bot \left( {ACD} \right)\)
Mà \(MN \in \left( {ACD} \right) \Rightarrow BM \bot MN\)