Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

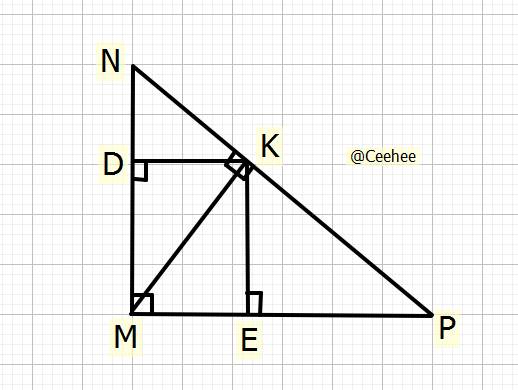
`a)` Biết `MN=7cm;NP=25cm`
Xét \(\Delta MNP\) vuông tại `M`, đường cao `MK`
Ta có: \(NP^2=MN^2+MP^2\) (đl Pytago)
\(\Rightarrow25^2=7^2+MP^2\\ \Rightarrow MP^2=25^2-7^2=576\\ \Rightarrow MP=\sqrt{576}=24cm\)
Ta có: \(\dfrac{1}{MK^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{MK^2}=\dfrac{1}{7^2}+\dfrac{1}{24^2}\\ \Rightarrow\dfrac{1}{MK^2}=\dfrac{625}{28224}\\ \Rightarrow MK^2=\dfrac{1\cdot28224}{625}\\ \Rightarrow MK=\sqrt{\dfrac{28224}{625}}\\ \Rightarrow MK=6,72cm\)
Ta có: \(MN^2=NK\cdot NP\left(htl\right)\)
\(\Rightarrow7^2=NK\cdot25\\ \Rightarrow NK=\dfrac{7^2}{25}=1,96cm\)
Vậy: \(MP=24cm;MK=6,72cm;NK=1,96cm\)
`b)` \(C/m:MD\cdot MN=ME\cdot MP\)
Xét \(\Delta KMN\) vuông tại `K`
Ta có: \(MK^2=MD\cdot MN\left(htl\right)\left(1\right)\)
Xét \(\Delta KMP\) vuông tại `K`
Ta có: \(MK^2=ME\cdot MP\left(htl\right)\left(2\right)\)
Từ `(1)` và `(2)` \(\Rightarrow MK^2=MK^2\)
\(\Rightarrow MD\cdot MN=ME\cdot MP\left(=MK^2\right)\)
(Câu `c)` tớ chịu :v).

Xét ΔMNP vuông tại M có MH là đường caop
nên \(NM^2=NH\cdot NP\)
=>\(NP\cdot7=10^2=100\)
=>\(NP=\dfrac{100}{7}\left(cm\right)\)
ΔMNP vuông tại M
=>\(MN^2+MP^2=NP^2\)
=>\(MP^2=NP^2-MN^2=\left(\dfrac{100}{7}\right)^2-10^2=\dfrac{5100}{49}\)
=>\(MP=\dfrac{10\sqrt{51}}{7}\left(cm\right)\)
\(\widehat{HMP}+\widehat{HMN}=90^0\)
\(\widehat{HMN}+\widehat{N}=90^0\)
=>\(\widehat{HMP}=\widehat{N}\)
Xét ΔMNP vuông tại M có \(sinN=\dfrac{MP}{NP}\)
=>\(sinHMP=\dfrac{10\sqrt{51}}{7}:\dfrac{100}{7}=\dfrac{\sqrt{51}}{10}\)

a: Xét ΔMAP vuông tại P có \(tanP=\dfrac{MA}{AP}=\dfrac{7}{4,5}=\dfrac{14}{9}\)
=>\(\widehat{P}\simeq57^0\)
b: Xét ΔMNP vuông tại M có MA là đường cao
nên \(MA^2=AN\cdot AP\)
=>\(AN\cdot4,5=7^2=49\)
=>\(AN=\dfrac{98}{9}\left(cm\right)\)
NP=NA+AP
\(=\dfrac{98}{9}+\dfrac{9}{2}=\dfrac{277}{18}\left(cm\right)\)
Xét ΔMNP vuông tại M có MA là đường cao
nên \(\left\{{}\begin{matrix}MN^2=NA\cdot NP\\MP^2=PA\cdot PN\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}MN=\sqrt{\dfrac{98}{9}\cdot\dfrac{277}{18}}=\dfrac{7\sqrt{277}}{9}\left(cm\right)\\MP=\sqrt{4,5\cdot\dfrac{277}{18}}=\dfrac{\sqrt{277}}{2}\left(cm\right)\end{matrix}\right.\)

Áp dụng hệ thức trong tam giác vuông có:
\(MP^2=PK.PN\Leftrightarrow PN=12,5\left(cm\right)\)
\(MN=\sqrt{PN^2-MP^2}=7,5cm\)
\(MN^2=NK.NP\Leftrightarrow NK=4,5\left(cm\right)\)
\(MK^2=KN.KP=4,5.8=36\Leftrightarrow MK=6\left(cm\right)\)
Vậy...
NP=MP^2/PN=10^2/8=12,5cm
MK=căn 10^2-8^2=6cm
NK=6^2/8=4,5cm
MN=căn 12,5^2-10^2=7,5cm

M N P K E F 1 1 1
mk chỉ nêu hướng giải còn bn tự trình bày nha
a,Ta có MN=3cm ,MP=4cm
=>NP=5cm
Ta có MN2=NK.NP (HỆ THỨC LƯỢNG TRONG TAM GIÁC MNP VUÔNG )
=>NK=32:5=1,8cm
T2 BN TÍNH ĐC KP
Lại có MK2=NK.KP (HỆ THỨC LƯỢNG TRONG TAM GIÁC MNP VUÔNG)
=>MK=2,4cm
Lại có MK2=MF.MP
=>MF=1,44cm
b, bn C/m MEKF là hcn =>\(\widehat{M_1}=\widehat{E_1}\)
Ta có \(\widehat{M_1}+\widehat{N}=90^O,\widehat{M_1}=\widehat{E_1}\)
=> \(\widehat{E_1}+\widehat{N}=90^O\)
Lại có \(\widehat{E_1}+\widehat{F_1}=90^O\)
\(\Rightarrow\widehat{F_1}=\widehat{N}\)=> \(\Delta EFM\)ĐỒNG DẠNG VS\(\Delta PNM\)(dpcm)
tk mk nha
chúc bn học giỏi

Áp dụng HTL: \(KN=\dfrac{MN^2}{NP}=5,4\left(cm\right)\)

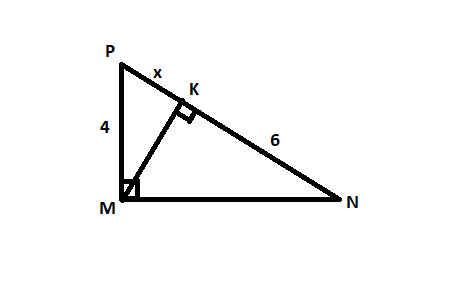
Xét ΔMNP vuông tại M có MK là đường cao
nên \(PM^2=PK\cdot PN\)
=>x(x+6)=16
=>x=2
Áp dụng định lý Py-ta-go cho tam giác MNP vuông tại M:
\(MN^2+MP^2=NP^2\)
Thay số: \(7^2+MP^2=25^2\)
\(\Rightarrow MP=24\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông MNP, đường cao MH ta có:
\(MK.NP=MN.MP\)
Thay số: \(MK.25=7.24\Rightarrow MK=6,72\left(cm\right)\)
Áp dụng định lý Py - ta - go cho tam giác MNK vuông tại K ta có:
\(MK^2+NK^2=MN^2\)
Thay số: \(6,72^2+NK^2=7^2\Rightarrow NK=1,96cm\)
thanks bn