Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(\widehat{NMH}+\widehat{N}=90^0\)
\(\widehat{P}+\widehat{N}=90^0\)
Do đó: \(\widehat{NMH}=\widehat{P}\)

a: BC=BH+CH
=4+6
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)
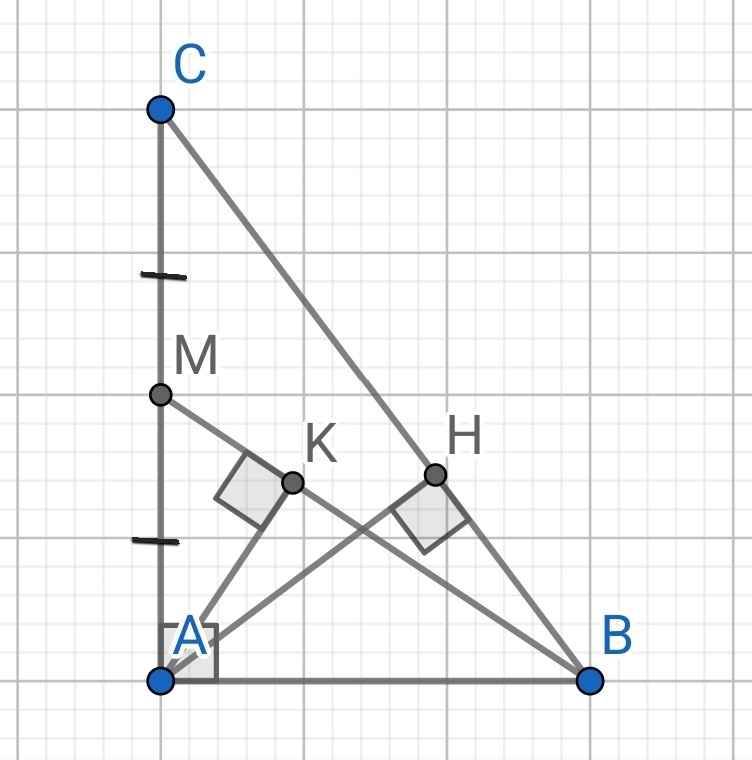
b: M là trung điểm của AC
=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)
=>\(\widehat{AMB}\simeq39^0\)
c: ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

BAN TU VE HINH NHA
a, trong tam giác MNK có \(\sin N=\frac{4}{5}\Rightarrow GOCN\approx53\)
ap dung dl pitago vao tam giac vuong MNK co \(NK^2+MK^2=NM^2\Rightarrow NK^2=5^2-4^2=3^2\Rightarrow NK=3\)
B, ap dung he thuc luong vao tam giac vuong MNK co \(MK^2=MC\cdot MN\)
tam giac vuong MKP co\(MK^2=MD\cdot MP\)
tu day suy ra MC*MN=MD*MP
C, ta co \(NP=NK+KP\)
ma \(NK=MK\cdot cotN\) \(KP=MK\cdot cotP\)
suy ra \(NP=MK\cdot\left(cotN+cotP\right)\)
D, ta co trong tam giac vuong MDK \(MD=MK\cdot cosM=4\cdot cos30=2\sqrt{3}\)
ma trong tam giac vuong MKP c o\(MK^2=MD\cdot MP\Rightarrow MP=\frac{4^2}{2\sqrt{3}}=\frac{8\sqrt{3}}{3}\)
lai co \(MD+DP=MP\Rightarrow DP=\frac{2\sqrt{3}}{3}\)

a: NP=NI+IP
=5+7=12(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên \(\left\{{}\begin{matrix}MN^2=NI\cdot NP\\MP^2=PK\cdot PN\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}MN=\sqrt{5\cdot12}=2\sqrt{15}\left(cm\right)\\MP=\sqrt{7\cdot12}=2\sqrt{21}\left(cm\right)\end{matrix}\right.\)
b: trung tâm là cái gì vậy bạn?
c: Nếu kẻ như thế thì H trùng với I rồi bạn
sửa lại chỗ câu b ghi lộn MP Chứ k phải NP