Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng các tỉ số lượng giác, tính được:
sinB = 3 5 ; cosB = 4 5 ; tanB = 3 4 ; cotB = 4 3
=> sinA = 4 5 ; cosA = 3 5 ; tanA = 4 3 ; cotA = 3 4

tam giác ABC ( A=90*)
=> \(AB=\sqrt{BC^2-AC^2}=\sqrt{1,2^2-0,9^2}\approx0,79\)( theo đlý pytago)
=> \(\sin B=\frac{AC}{BC}=\frac{0,9}{1,2}\approx1,14\)\(\Rightarrow\sin B=\cos A\approx1,14\)
\(\Rightarrow\cos B=\frac{AB}{BC}=\frac{0,79}{1,2}\approx0,66\Rightarrow\cos B=\sin A\approx0,66\)
\(\Rightarrow\tan B=\frac{AC}{AB}=\frac{0,9}{0,79}\approx1,139\Rightarrow\tan B=\cot A\approx1,139\)
\(\Rightarrow\cot B=\frac{AB}{AC}=\frac{0,79}{0,9}\approx0,87\Rightarrow\cot B=\tan A\approx0,87\)

Áp dụng định lí pytago vào Δvuông ABC có:
AB²=AC²+BC²=0,9²+1,2²=2,25
⇒AB=1,5(cm)
Có góc A và góc B phụ nhau, ta có:
sin B = cosA= AC/AB = 3/5
cos B = sin A = BC/AB = 4/5
tan B = cot A = AC/BC = 3/4
cot B = tan A = BC/AC = 4/3
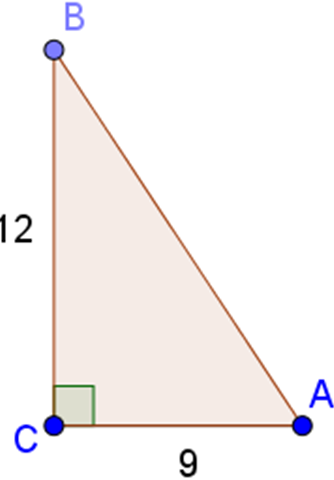
Ta có: AC = 0,9m = 9dm; BC = 1,2m = 12dm
Theo định lí Pitago, ta có:
Vì ∠A và ∠B là hai góc phụ nhau nên suy ra:
Bạn tham khảo nha

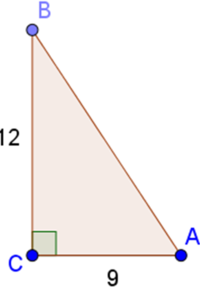
Ta có: AC = 0,9m = 9dm; BC = 1,2m = 12dm
Theo định lí Pitago, ta có:

Vì ∠A và ∠B là hai góc phụ nhau nên suy ra:
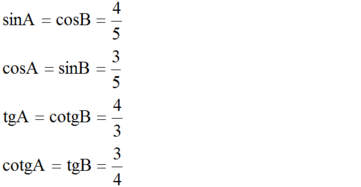
(Ghi chú: Các bạn nên đổi đơn vị như trên để việc tính toán trở nên dễ dàng hơn.)

sinA=cosB=0,8sinA=cosB=0,8
cosA=sinB=0,6cosA=sinB=0,6
tgA=cotgB=43≈1,33tgA=cotgB=43≈1,33
cotgA=tgB=0,75cotgA=tgB=0,75.

\(\sin\widehat{B}=\cos\widehat{A}=\dfrac{AC}{AB}=\dfrac{3}{5}\)
\(\cos\widehat{B}=\sin\widehat{A}=\dfrac{4}{5}\)
\(\tan\widehat{B}=\cot\widehat{A}=\dfrac{3}{4}\)
\(\cot\widehat{B}=\tan\widehat{A}=\dfrac{4}{3}\)

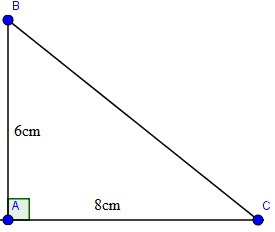
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+82=100BC2=AB2+AC2=62+82=100
Suy ra: BC = 10 (cm)
Ta có:
sinˆB=ACBC=810=0,8sinB^=ACBC=810=0,8
cosˆB=ABBC=610=0,6cosB^=ABBC=610=0,6
tgˆB=ACAB=86=43tgB^=ACAB=86=43
cotgˆC=tgˆB=43

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10 (cm)
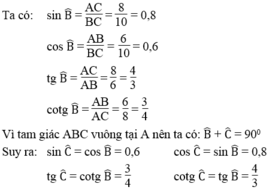

\(BC^2=AB^2+AC^2=36+64=100=10^2\)
\(\Rightarrow BC=10\left(cm\right)\)
\(SinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\Rightarrow SinC=Sin\left(90-B\right)=CosB=\dfrac{3}{5}\)
\(CosB=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\Rightarrow CosC=Cos\left(90-B\right)=SinB=\dfrac{4}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\Rightarrow tanC=tan\left(90-B\right)=CotB=\dfrac{3}{4}\)
\(CotB=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\Rightarrow cotC=cot\left(90-B\right)=tanB=\dfrac{4}{3}\)
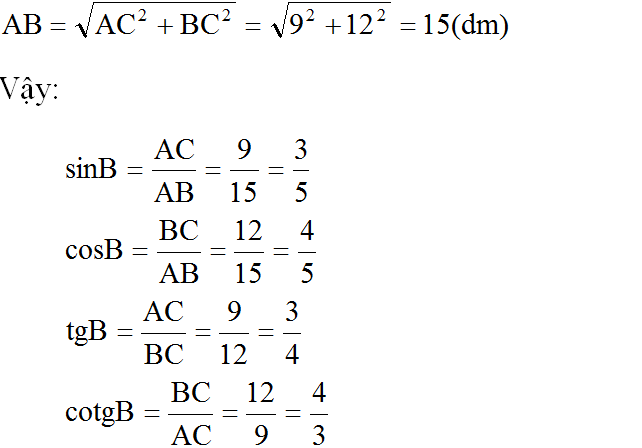
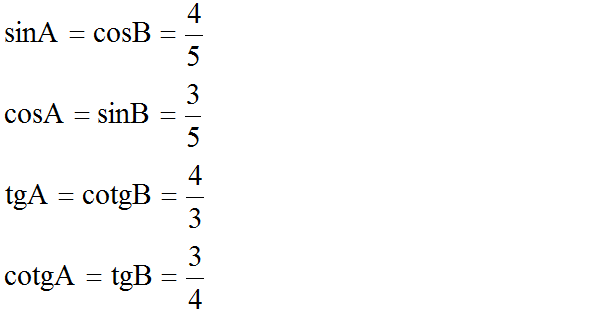

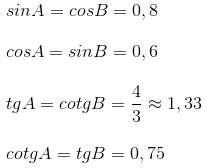
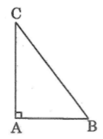
Áp dụng định lý Pitago:
\(AB=\sqrt{AC^2+BC^2}=1,5\left(cm\right)\)
\(sinB=\dfrac{AC}{AB}=0,6\) \(\Rightarrow cosA=sinB=0,6\)
\(cosB=\dfrac{BC}{AB}=0,8\) \(\Rightarrow sinA=cosB=0,8\)
\(tanB=\dfrac{AC}{BC}=\dfrac{3}{4}\) \(\Rightarrow cotA=tanB=\dfrac{3}{4}\)
\(cotB=\dfrac{BC}{AB}=\dfrac{4}{3}\) \(\Rightarrow tanA=cotB=\dfrac{4}{3}\)