Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha.
a,Xét tg ABE và tg HBE:
^BAE=^BHE=90*
^ABE=^HBE(BE là pg)
BE chung
=>tg ABE= tg HBE(ch-gn)
b,+,tg ABC có:^BAC=90*,^ABC=60*
=>^C=30*
+,tg BHE có: ^BHE=90*,^EBH=30*(^EHB=1/2ABC)
=>^HEB=60*
Mà HK // BE
=>^HBE=^EHK=60*(slt)
+, tg CHE có:^EHC=90*,^C=30*
=>HEC=60*
+,tg HEK có:
^EHK=60*,^HEC(^HEK)=60*
=>TG HEK đều(dhnb)
Phần c mik chỉ ghi các bước thôi còn bạn tự chình bày nhé.
c, +,CM:tg AEM=tg HEC(cgv-gnk)
=>AM=HC
+,CM:BM=BC
+,CM:tg BMI=tgBCI(cgc)
=>NM=NC
Xong r nha. Chúc bạn học tốt.

Bài 5:
a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)

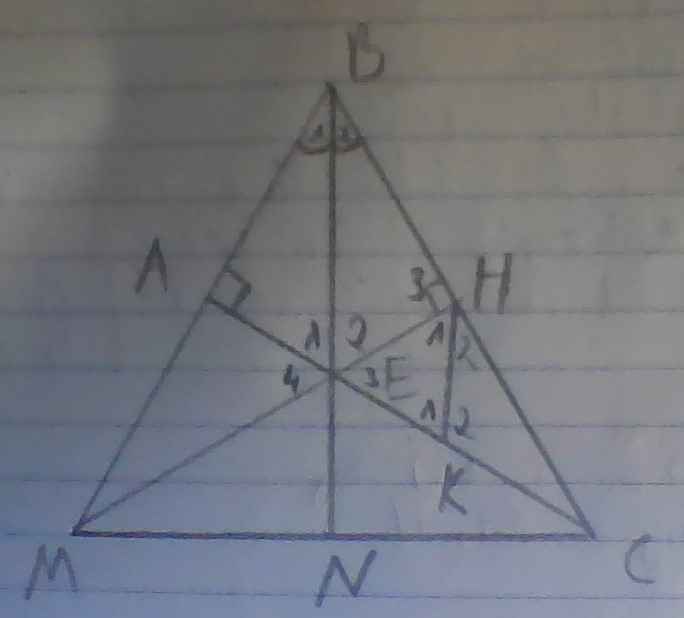
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC

a) Ta có ^BEA = 90 - ^ ABE
^BEH = 90 - ^EBH
mà ^ABE = ^EBH ( do BE là tia phân giác)
=> ^BEA=^BEH
Xét tam giác ABE và Tam giác HBE có
^ABE=^BEH (gt)
BE chung
^BEA=^BEH (cmt)
=> tam giác ABE=Tam giác HBE
b) chỉ cần chứng minh BE là đườn trug tuyến là xog

Bạn tự vẽ hình nhé. Tại mình thấy đề AH vuông góc BC hơi sai nên sẽ sửa là EH nha.
Giải
a, Vì EH \(\perp BC\)( gt ) \(\Rightarrow\)\(\Delta HBE\)vuông tại H.
Xét \(\Delta\)vuông ABE và \(\Delta\) vuông HBE, có :
BE : cạnh chung
góc ABE = góc HBE ( BE là tpg góc ABC )
\(\Rightarrow\)\(\Delta\)vuông ABE = \(\Delta\) vuông HBE ( cạnh huyền góc nhọn )
b, Ta có : BA=BH ( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE ) \(\Rightarrow\) \(\Delta BAH\) cân tại B ( đ/n )
Mà góc ABC = 60o ( gt ) \(\Rightarrow\) \(\Delta BAH\) đều.
\(\Rightarrow\)AB=AH=BH ( đ/n )
Xét \(\Delta\) vuông ABC, có :
góc ABC + góc BCA = 90o ( 2 góc phụ nhau )
\(\Rightarrow\)60o + góc BCA = 90o \(\Rightarrow\)góc BCA = 30o
Mà góc EBH = 30o ( vì BE là tpg góc ABC , góc ABC = 60o )
\(\Rightarrow\)góc EBC = góc BCA ( =30o )
\(\Rightarrow\)\(\Delta\)BEC cân tại E ( t/c ) \(\Rightarrow\)BE = EC ( đ/n )
Xét \(\Delta\) vuông HEB và \(\Delta\) vuông HEC , có :
BE=EC ( cmt )
góc EBH = góc ECH ( cmt )
\(\Rightarrow\)\(\Delta\)vuông HEB = \(\Delta\) vuông HEC ( cạnh huyền góc nhọn )
\(\Rightarrow\)BH = CH ( 2 cạnh tương ứng )
c, Xét \(\Delta\) vuông ABE , có :
góc ABE + góc AEB = 90o ( 2 góc phụ nhau ), mà góc ABE = 30o ( BE là tpg góc ABC )
\(\Rightarrow\)góc AEB = 60o
Ta có : góc AEB = góc HEB = 60O( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE )
Mà BE // HK ( gt ) \(\Rightarrow\) góc HEB = góc EHK = 60o( 2 góc so le trong )
Vì BE // HK ( gt ) \(\Rightarrow\) góc AEB = góc EKH = 60o ( 2 góc đồng vị )
Xét \(\Delta EHK\) , có :
góc EHK + góc EKH + góc KEH = 180o ( tổng 3 góc trong tam giác )
\(\Rightarrow\)60o + 60o + góc KEH = 180o
\(\Rightarrow\)góc KEH = 60o
Ta nhận thấy trong tam giác EKH cả 3 góc đều bằng 60o ( cmt )
\(\Rightarrow\)\(\Delta EKH\)là tam giác đều ( t/c)
d, Xét \(\Delta\) AEI và \(\Delta HEC\) , có :
góc EAI = góc EHC ( = 900 )
AE=EH ( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE )
góc AEI = góc HEC ( 2 góc đối đỉnh )
\(\Rightarrow\Delta AEI=\Delta HEC\)( g-c-g )
\(\Rightarrow\)EI = EC ( 2 cạnh tương ứng )
Xét \(\Delta\) vuông HEC, có :
EC > EH ( cạnh huyền > cạnh góc vuông ) , mà EC = EI ( cmt )
\(\Rightarrow\)EI hay IE > EH ( đpcm )

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D