Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N H E D I I
Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)

Cho tam giác ABC vuông tại A, có AB < AC. Kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: HB < AH < HC.
b) Tia phân giác góc BAH cắt BC tại D. Qua C kẻ đường thẳng vuông góc với AD và cắt AD tại I.
Chứng minh: CI là tia phân giác của góc ACB.
c) Tia phân giác góc ADC cắt CI tại K, từ K vẽ KE vuông góc với BC (K thuộc BC).
Chứng minh: ID + IC > KE+ DC.
Câu hỏi tương tự Đọc thêm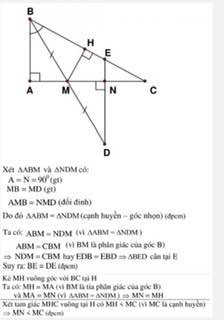
A B C D I
TA CÓ:\(\frac{AD}{CD}=\frac{AB}{BC}\)VÌ BD LÀ PHÂN GIÁC CỦA (1)
VÌ \(AB\perp AC\left(gt\right)\)
VÀ \(CI\perp AC\left(gt\right)\)
NÊN \(AB//CI\)
\(\Rightarrow\frac{AD}{DC}=\frac{AB}{CI}\)(HỆ QUẢ ĐỊNH LÍ TA-LET) (2)
TỪ (1) VÀ (2) \(\Rightarrow\frac{AB}{BC}=\frac{AB}{CI}\)
\(\Rightarrow BC=CI\)
MÀ AB<BC VÀ AC<BC (VÌ BC LÀ CẠNH HUYỀN CỦA TAM GIÁC VUÔNG ABC)
DO ĐÓ AB<CI VÀ AC<CI
HỌC TỐT