Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BCEDAF
*Hình quên đánh dấu ABD = DBE nhé
*Cần viết gt và kl thì bảo mình nhá <3
Giải
a) Xét ∆ABD và ∆EBD có :
AB = BE (gt) |
FBD = DBE (AD là tia phân giác ABE) }
BD là cạnh chung |
=> ∆ABD = ∆EBD (c.g.c)

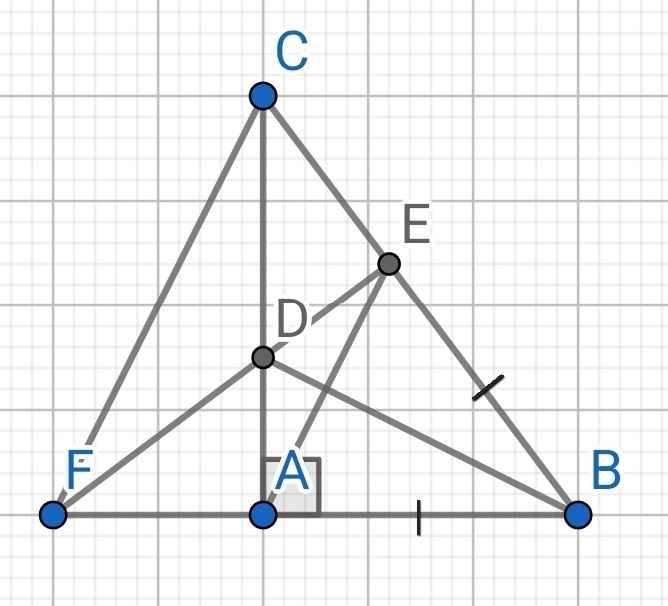 a) Xét ∆ABD và ∆EBD có:
a) Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (BD là tia phân giác của ABC)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
Lại do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ ∠DAF = ∠DEC = 90⁰
Xét hai tam giác vuông: ∆DAF và ∆DEC có:
AD = ED (cmt)
∠ADF = ∠EDC (đối đỉnh)
⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = EC (hai cạnh tương ứng)
c) ∆BAE có:
AB = BE (gt)
⇒ ∆BAE cân tại B
⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2 (1)
Do AF = EC (cmt)
AB = BE (gt)
⇒ AF + AB = EC + BE
⇒ BF = BC
⇒ ∆BFC cân tại B
⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2 (2)
Từ (1) và (2) suy ra:
∠BEA = ∠BCF
Mà ∠BEA và ∠BCF là hai góc đồng vị
⇒ AE // CF

`Answer:`

a. Vì `\triangleABC` vuông tại `A` nên theo định lí Pytago, ta có:
\(AB^2=BC^2-AC^2\Leftrightarrow AB^2=13^2-12^2\Leftrightarrow AC^2=169-144=25\Leftrightarrow AC=5cm\)
b. Xét `\triangleABD` và `\triangleEBD:`
`BD` chung
`BA=BE`
`\hat{ABD}=\hat{EBD}`
`=>\triangleABD=\triangleEBD(c.g.c)`
c. Theo phần b. `\triangleABD=\triangleEBD`
`=>\hat{BAD}=\hat{BED}=90^o`
`=>DE⊥BC`
d. Xét `\triangleADF` và `triangleEDC:`
`AD=DE`
`\hat{DAF}=\hat{DEC}=90^o`
`\hat{ADF}=\hat{EDC}`
`=>\triangleADF=\triangleEDC(g.c.g)`
`=>AF=BC`

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)

Xét ΔABDΔABD và ΔEBDΔEBD, ta có:
AB=BE ( gt)
ABDˆ=EBDˆABD^=EBD^ ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD⇒ΔABD=ΔEBD (c-g-c)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc ABD=góc EBD
=>BD là phân giác của góc ABE
c: Xét ΔBEM vuông tại E và ΔBAC vuôg tại A có
BE=BA
góc EBM chung
=>ΔBEM=ΔBAC
=>BM=BC


B E C A D F
Xét \(\Delta ABD\) và \(\Delta EBD\)
ta có DA = DE ( gt )
BA = BE ( gt )
BD là cạnh chung
=> \(\Delta ABD=\Delta EBD\left(c.c.c\right)\)