Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K M N
Áp dụng hệ thức lượng trong tam giác vuông ta có : AB^2 = BC . KB => \(AB=\sqrt{BC.KB}=\sqrt{5}.\)( cm )
Tương tự AC = \(2\sqrt{5}\)(cm )
b, Tứ giác AMKN có 3 góc vuông => AMKN là hình chữ nhật => MN = AK ( 2 đường chéo hcn bằng nhau )
=> MN = AK = ( AB . AC ) : BC = 2 ( cm )

Áp dụng hệ thức lượng:
\(AK^2=BK.CK=9.4=36\)
\(\Rightarrow AK=6\left(cm\right)\)
Áp dụng định lý Pitago:
\(AB^2=AK^2+BK^2\Rightarrow AB=\sqrt{AK^2+BK^2}=3\sqrt{13}\left(cm\right)\)
\(AC=\sqrt{AK^2+CK^2}=2\sqrt{13}\left(cm\right)\)

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

-
a) Ta có:
- Diện tích tam giác ABC là S = 1/2 * AB * AC = 1/2 * 3cm * 4cm = 6cm^2.
- Vì AD là đường cao của tam giác ABC nên diện tích tam giác ABC cũng bằng 1/2 * AB * CD, tức là: S = 1/2 * AB * CD = 3CD.
Từ đó suy ra: CD = 2cm.
b) Gọi E là hình chiếu vuông góc của D trên BC. Ta có:
-
Tam giác ADE và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AB.
-
Tam giác BDE và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AC.
Do đó, ta có: -
AI/AB = DE/BC (vì tam giác ADE và tam giác ABC đồng dạng)
-
DE = AD - AE = AD - CD = AD - 2 (vì tam giác ADE vuông tại E và CD là hình chiếu của AD trên BC)
-
BC = AB + AC = 3 + 4 = 7
Từ đó suy ra: AI/AB = (AD - 2)/7
Vậy, ta có: AI*AB = (AD - 2)AB/7 = ADAB/7 - 2AB/7 = AD^2/3 - 2/7.
c) Gọi F là hình chiếu vuông góc của D trên AB. Ta có:
-
Tam giác ADF và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AB.
-
Tam giác CDF và tam giác ABC đồng dạng với tỉ số đồng dạng CD/AC.
Do đó, ta có: -
AI/AB = DF/AF (vì tam giác ADF và tam giác ABC đồng dạng)
-
AK/AC = CF/AF (vì tam giác CDF và tam giác ABC đồng dạng)
-
DF + CF = CD = 2
-
AF = AB - BF = AB - AK = 3 - AK (vì BF là hình chiếu của B trên AC và AK là hình chiếu của D trên AC)
Từ đó suy ra: AI/AB = DF/(DF + CF) = DF/2 = (AD^2 - AF^2)/(2AD^2) = (AD^2 - (AB - AK)^2)/(2AD^2) = (2AK*AC - AK^2)/(2AD^2) = AK/AD - AK^2/(2AD^2).
Từ b) và c), ta có: AIAB = AD^2/3 - 2/7 = AKAC*(1 - AK^2/(2AD^2)).
d) Gọi H là hình chiếu vuông góc của I trên BC. Ta có:
-
Tam giác ADH và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AB.
-
Tam giác IDH và tam giác ABC đồng dạng với tỉ số đồng dạng AI/AC.
Do đó, ta có: -
ID/AI = DH/AB (vì tam giác IDH và tam giác ABC đồng dạng)
-
DH = CD - CH = 2 - CI (vì tam giác ADH vuông tại H và CI là hình chiếu của I trên BC)
-
AB = 3, AC = 4, BC = 7
Từ đó suy ra: ID/AI = (CD - CH)/AB = (2 - CI)/3.
Do đó, ta có: ID/AI = (2 - CI)/3 = (2 - AK)/4 (vì AIAB = AKAC từ c))
Từ đó suy ra: ID = (2AI - 3AK)/4.
Vậy, ta có: ID/AI = (2AI - 3AK)/(4AI) = 1 - 3AK/(2AI) = 1 - DH
18:22
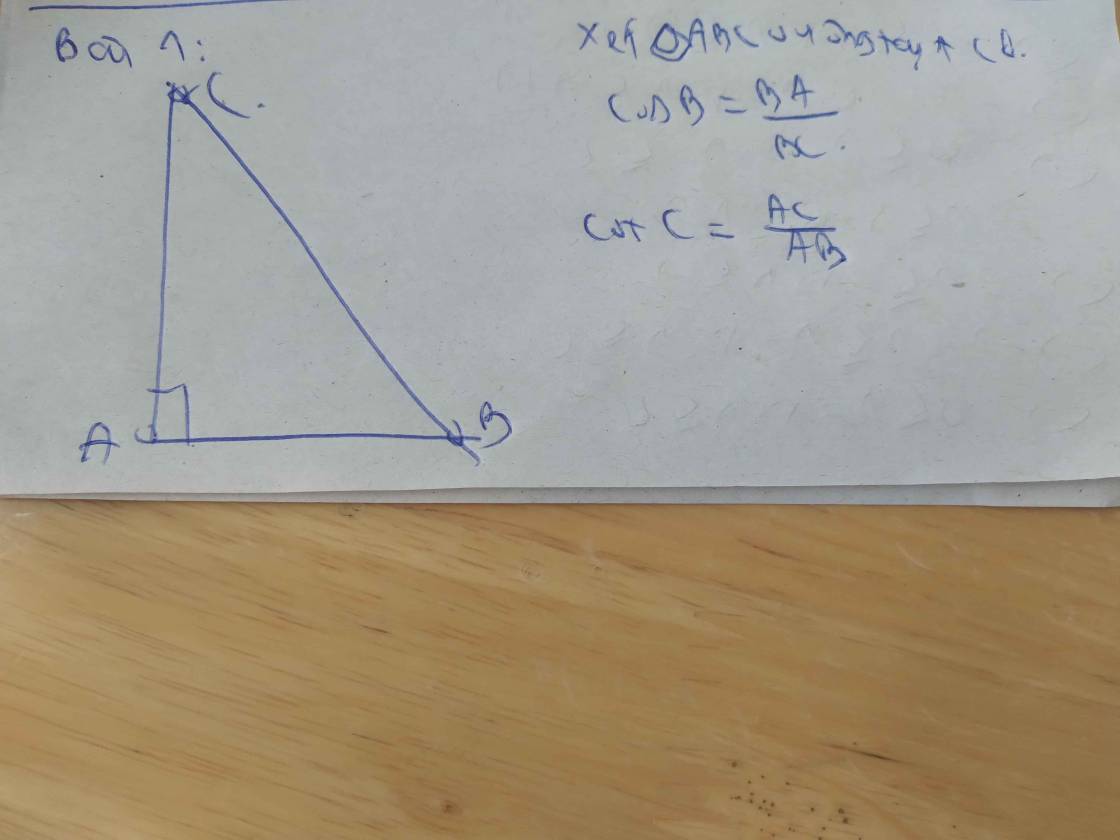

Hình như ko đủ dữ kiện
Chỉ cần áp dụng hệ thức lượng trong tam giác vuông là ra liền (tự ghi rõ lời giải)
a)
\(AK^2=KC.BK=9.4\Rightarrow AK=6\left(cm\right).\)
b)
\(AB^2=AK^2+BK^2=6^2+4^2\Rightarrow AB=2\sqrt{13}\left(cm\right)\)(Định lý Pytago)
\(AC^2=AK^2+KC^2=6^2+9^2\Rightarrow AC=3\sqrt{13}\left(cm\right)\)