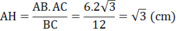Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=92+122=225
BC=15cm
* AH.BC=AB.AC
AH.15=9.12
AH.15=108
AH=7,2cm
\(sinB=\dfrac{4}{5};cosB=\dfrac{3}{5};tanB=\dfrac{4}{3};cotanb=\dfrac{3}{4}\)
\(=>sinC=\dfrac{3}{5};cosC=\dfrac{4}{5};tanC=\dfrac{3}{4};cotanC=\dfrac{4}{3}\)
b)
tam giác ABC vuông tại A có
AC.AK=AH2
HB.HC=AH2
=>AC.AK=HB.HC
\(=>\dfrac{AC}{HC}=\dfrac{HB}{AK}\)
b) Xét tam giác ABC vuông tại A có đường cao AH
⇒ A B 2 = BH.BC
A C 2 = CH.CB
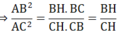
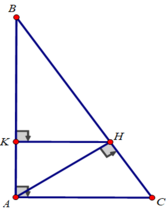
a) Xét tam giác ABC vuông tại A có đường cao AH
⇒ AH2 = HC.HB (1)
Xét tam giác AHB vuông tại H có đường cao HK
⇒ A H 2 = AK.AB (2)
Từ (1) và (2) ⇒ AK.AB = HC.HB
GIẢI: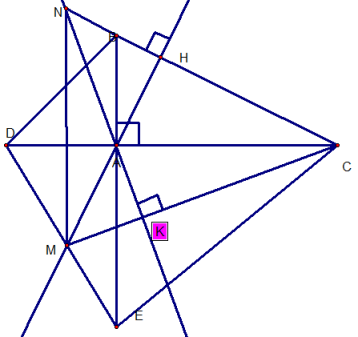
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
c) Xét tam giác ABC vuông tại A có ∠B = 30 0 , AC = 6 cm:
AB = AC.cotgB = 6.cotg 30 0 = 2 3 (cm)
AC = BC.sinB ⇒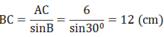
Tam giác ABC vuông tại A có AH là đường cao nên
AH.BC = AB.AC ⇒