Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B C M E D 1 2 3 4 A N 1 2 1 2 1 2 1 2 1 2 I
tg là tam giác nha !
a )
Ta có : gócA1 + gócBAC = gócDAC ( AB nằm giữa AD và AC )
=> gócA1 = gócDAC - gócBAC = 90o - gócBAC ( 1 )
Ta có : gócA2 + gócBAC = gócBAE ( AC nằm giữa AB và AE )
=> gócA2 = gócBAE - gócBAC = 90o - gócBAC ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : gócA1 = gócA2 .
Xét tgABD và tgACE , có :
AD = AC ( gt )
AB = AE ( gt )
gócA1 = gócA2 ( cmt )
Do đó : tgABD = tgACE ( c - g - c )
=> BD = CE ( 2 cạnh tương ứng ) .
b ) Xét tgABM và tgNCM , có :
gócM1 = gócM2
BM = CM ( AM là trung tuyến)
AM = NM ( gt )
Do đó : tgABM = tgNCM ( c - g - c )
=> gócC1 = gócB1 ( 2 góc tương ứng )
Mà : gócB1 = gócADC + gócA1 ( góc ngoài của tg bằng tổng 2 góc trong không kề với nó )
Do đó : gócC1 = gócADC + gócA1
Ta có : gócC2 + gócDAC + gócADC = 180o ( tổng 3 góc trong tg )
=> gócC2 = 180o - gócDAC - gócADC = 180o - 90o - gócADC = 90o - gócADC
Ta có : gócACN = gócC1 + gócC2 ( DC nằm giữa AC và NC )
=> gócACN = ( gócADC + gócA1 ) + ( 90o - gócADC ) = gócADC + gócA1 + 90o - gócADC = 90o + gócA1 ( 3 )
Ta có : gócDAE = gócBAE + gócA1 ( AB nằm giữa AD và AE )
=> gócDAE = 90o + gócA1 ( 4 )
Từ ( 3 ) và ( 4 ) suy ra : gócACN = gócDAE ( 5 )
Ta có : tgABM = tgNCM ( cmt )
=> AB = CN ( 2 cạnh tương ứng )
Mà : AB = AE ( gt )
Do đó : CN = AE ( 6 )
Xét tgADE và tgACN , có :
AD = AC ( gt )
AE = CN ( cmt ( 6 ) )
gócACN = gócDAE ( cmt ( 5 ) )
Do đó : tgADE = tgACN ( c - g - c )
c ) Nằm ngoài khả năng của mình rồi !
Học tốt nha !

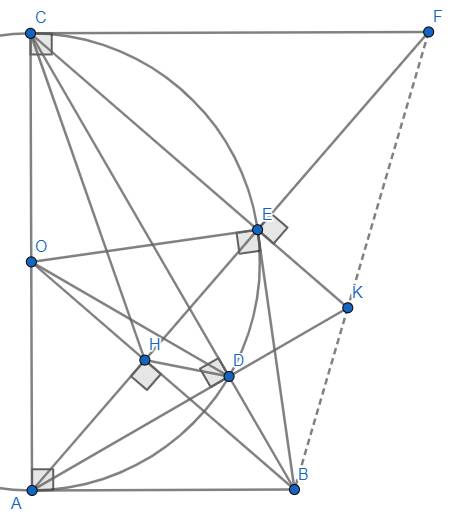
a) a1. Chứng minh \(BAOE\) là tứ giác nội tiếp.
Tứ giác \(BAOE:\left\{{}\begin{matrix}\hat{OEB}=90^o\left(\text{tiếp tuyến}\right)\\\hat{OAB}=90^o\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{OEB}+\hat{OAB}=90^o+90^o=180^o\Rightarrow BAOE\) là tứ giác nội tiếp (đpcm).
a2. Chứng minh : \(BH.BO=BD.BC\).
Ta có : \(\hat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BD.BC=AB^2\left(1\right).\)
Mặt khác : \(\left\{{}\begin{matrix}OA=OE=R\left(gt\right)\\AB=BE\left(\text{tính chất hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OB\) là đường trung trực của \(AE\Rightarrow\hat{AHB}=90^o\)
\(\Rightarrow AH\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BH.BO=AB^2\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BH.BO=BD.BC\) (đpcm).
b) b1. Chứng minh \(DHOC\) là tứ giác nội tiếp.
Tứ giác \(AHDB:\hat{AHB}=\hat{ADB}=90^o\left(cmt\right)\). Mà hai góc này có đỉnh kề nhau trong tứ giác và cùng nhìn cạnh \(AB\) nên đây là tứ giác nội tiếp \(\Rightarrow\hat{ABH}=\hat{ADH}.\)
Mà : \(\left\{{}\begin{matrix}\hat{ADH}+\hat{HDC}=90^o\left(=\hat{ADC}\left(cmt\right)\right)\\\hat{ABH}+\hat{HAB}=90^o\left(\text{hai góc phụ nhau}\right)\end{matrix}\right.\Rightarrow\hat{HDC}=\hat{HAB}\left(3\right).\)
Mặt khác : \(\hat{AOB}=\hat{HAB}\left(\text{cùng phụ }\hat{ABH}\right)\left(4\right).\)
Từ \(\left(3\right),\left(4\right)\Rightarrow\hat{AOB}=\hat{HDC}\Rightarrow DHOC\) là tứ giác nội tiếp (dấu hiệu nhận biết) (đpcm).
b2. Chứng minh : \(\hat{BHD}=\hat{OHC}\).
Do \(DHOC\) là tứ giác nội tiếp (cmt) \(\Rightarrow\hat{OCD}=\hat{BHD}\left(5\right)\) (cùng bù với \(\hat{OHD}\)) và \(\hat{OHC}=\hat{ODC}\left(6\right)\) (hai góc có đỉnh kề nhau cùng nhìn cạnh \(OC\)).
Mặt khác : \(OA=OD=R\Rightarrow\Delta OAD\) cân tại \(O\Rightarrow\hat{ODA}=\hat{OAD}.\)
Và : \(\left\{{}\begin{matrix}\hat{OAD}+\hat{OCD}=90^o\left(\text{hai góc phụ nhau}\right)\\\hat{ODA}+\hat{ODC}=90^o\left(=\hat{ADC}\right)\end{matrix}\right.\Rightarrow\hat{OCD}=\hat{ODC}\left(7\right).\)
Từ \(\left(5\right),\left(6\right),\left(7\right)\Rightarrow\hat{BHD}=\hat{OHC}\) (đpcm).
c) Chưa nghĩ ra ạ:)