Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có : NB = NC
=> tam giác NBC cân tại N
Có : NM vừa là đường trung tuyến vừa là đường cao
=> NM vuông góc với BC
Xét tam giác NMB và tam giác NMC có:
NM = NC
Cạnh NM chung
Góc NMB = NMC = 900
=> tám giác NMB = NMC (cạnh huyền cạnh góc vuông) (đpcm)
xét tam giác NMB và tam giác NMC ta có:
NB=NC(gt)
BM=MC(gt)
MN:cạnh chung
kết hợp ba cái trên . Suy ra tam giác NMB=tam giác NMC

Xét hai tam giác NMB và NMC có:
BM=MC (vì M là trung điểm)
NM là cạnh chung
NB=NC(gt)
=> tam giác NMB= tam giác NMC \(\left(\Delta\right)\)
Chúc bạn học tốt !!!

1.
Xét tam giác AMB và tam giác NMC có:
AM = NM (gt)
AMB = NMC (2 góc đối đỉnh)
MB = MC (M là trung điểm của BC)
=> Tam giác AMB = Tam giác NMC (c.g.c)
Xét tam giác AMC và tam giác NMB có:
AM = NM (gt)
AMC = NMB (2 góc đối đỉnh)
MC = MB (M là trung điểm của BC)
=> Tam giác AMC = Tam giác NMB (c.g.c)
2.
Xét tam giác AME và tam giác BMC có:
AM = BM (M là trung điểm của AB)
AME = BMC (2 góc đối đỉnh)
ME = MC (gt)
=> Tam giác AME = Tam giác BMC (c.g.c)
=> AEM = BCM (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AE // BC
Xét tam giác ANF và tam giác CNB có:
AN = CN (N là trung điểm của AC)
ANF = CNB (2 góc đối đỉnh)
NF = NB (gt)
=> Tam giác ANF = Tam giác CNB (c.g.c)
=> AF = CB (2 cạnh tương ứng)
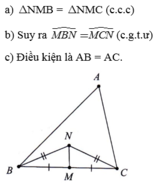
Hình bạn tự vẽ đc chớ nhỉ
a) Xét \(\Delta\) MNB và \(\Delta\) MNC có
MN : cạnh chung
MB = MC ( do M là trung điểm của BC )
NB = NC ( gt)
=>\(\Delta\) MNB = \(\Delta\)MNC ( c-c-c)
b) Theo câu a ta có
\(\Delta\) MNB = \(\Delta\)MNC
=> \(\widehat{NMB}=\widehat{NMC}\) ( 2 góc tương ứng ) (1)
Mà \(\widehat{NMB}+\widehat{NMC}=180^o\) ( 2 góc kề bù ) (2)
Từ (1) và (2) => \(\widehat{NMB}=\widehat{NMC}=\frac{180^o}{2}=90^o\) (*1)
Lại có MN cắt BC tại M (*2)
Từ (*1) và (*2) => \(MN\perp BC\) tại M
@@ Học tốt
Takigawa Miu_