Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

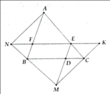
a) Kéo dài MP, NP lần lượt cắt BC tại E, D.
Xét tam giác ABC có ME // AC \(\Rightarrow\)\(\frac{AM}{AB}\)= \(\frac{CE}{BC}\)(1)
Xét tam giác ABC có ND // AB \(\Rightarrow\)\(\frac{AN}{AC}\)= \(\frac{BD}{BC}\)(2)
Xét tam giác ABQ có PD//AB \(\Rightarrow\frac{PQ}{AQ}=\frac{DQ}{BQ}\)
Xét tam giấc ACQ có PE//AC\(\Rightarrow\frac{PQ}{AQ}=\frac{QE}{QC}\)
\(\Rightarrow\frac{PQ}{AQ}=\frac{DQ}{BQ}=\frac{QE}{QC}=\frac{DQ+QE}{BQ+QC}=\frac{DE}{BC}\)(3)
Từ (1), (2), (3) suy ra \(\frac{AM}{AB}+\frac{AN}{AC}+\frac{PQ}{AQ}=\frac{CE}{BC}+\frac{DB}{BC}+\frac{DE}{BC}=1\)(đpcm)

Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng k: Đoạn thẳng [E, M] Đoạn thẳng l: Đoạn thẳng [F, M] A = (-1.14, 6.85) A = (-1.14, 6.85) A = (-1.14, 6.85) B = (-3.22, 3.05) B = (-3.22, 3.05) B = (-3.22, 3.05) C = (4.24, 2.98) C = (4.24, 2.98) C = (4.24, 2.98) Điểm M: Điểm trên g Điểm M: Điểm trên g Điểm M: Điểm trên g Điểm E: Giao điểm của i, f Điểm E: Giao điểm của i, f Điểm E: Giao điểm của i, f Điểm F: Giao điểm của j, h Điểm F: Giao điểm của j, h Điểm F: Giao điểm của j, h
a. Do ME // AC nên \(\frac{ME}{AC}=\frac{BM}{BC}\); MF // AB nên \(\frac{MF}{AB}=\frac{MC}{BC}\)
Từ đó suy ra \(\frac{ME}{AC}+\frac{MF}{AB}=\frac{BM+MC}{BC}=1\) không đổi.
b. Gọi \(\frac{ME}{AC}=t\Rightarrow\frac{MF}{AB}=1-t\Rightarrow S_{ABC}=\frac{a^2}{t^2}=\frac{b^2}{\left(1-t\right)^2}\)
\(\Rightarrow\frac{a}{t}=\frac{b}{1-t}\Rightarrow a\left(1-t\right)=bt\Rightarrow t=\frac{a}{a+b}\Rightarrow t^2=\frac{a^2}{\left(a+b\right)^2}\Rightarrow S_{ABC}=\frac{a^2}{t^2}=\left(a+b\right)^2.\)
c. \(S_{AEMF}=S_{ABC}-S_{BME}-S_{CMF}=\left(a+b\right)^2-a^2-b^2\)
\(=2ab\le a^2+b^2\)
Dấu bằng xảy ra khi a = b, tức là M là trung điểm BC.

a) Chứng minh được MN//PQ (cùng vuông góc với AC). Chứng minh được MP = QN. Þ ĐPCM.
b) Ta có:
S M N E = 1 2 S M E N C , S N P E = 1 2 S P B N E , S P Q E = 1 2 S , A P E Q S M Q E = 1 2 S Q E M D ⇒ S M N P Q = 1 2 S A B C S .
c) Chu vi MNPQ = MN + PQ + NP + QM
= EC + AE + BE + ED = AC + BE + ED.
Trong tam giác BED, BE + ED ³ BD
Þ Chu vi MNPQ ≥ AC + BD
Þ E là tâm của hình vuông ABCD