Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lí về đường trung bình của tam giác để chứng minh MI = IN = NK = KM (cùng bằng \(\dfrac{BD}{2}\) và \(\dfrac{CE}{2}\) )
MINK là hình thoi nên \(IK\perp MN\)

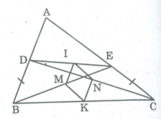
*Trong ∆ BCD,ta có:
K là trung điểm của BC (gt)
N là trung điểm của CD (gt)
Nên NK là đường trung bình của ∆ BCD
⇒ NK // BD và NK = 1/2 BD (1)
*Trong ∆ BED,ta có:
M là trung điểm của BE (gt)
I là trung điểm của DE (gt)
Nên MI là đường trung bình của ∆ BED
⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)
Từ (1) và (2) suy ra: MI // NK và MI = NK
Nên tứ giác MKNI là hình bình hành.
*Trong ∆ BEC ta có MK là đường trung bình.
⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)
BD = CE (gt). Suy ra: MK = KN
Vậy hình bình hành MKNI là hình thoi.
⇒IK ⊥ MN (t/chất hình thoi).
a) vì DNBI là hbh => DN = BI
cmtt NE = KC
mà DN = NE
=> BI = KC(1)
ta có KC song song vs NE ( hbh) , BI song song vs DN (hbh) mà DN và NE thg hàng => BI song song vs KC (2)
Từ 1 và 2 => BIKC là hbh
ta có BC là đg chéo của hbh BIKC mà M là tđ của BC
=> đg chéo IK đi qua trung điểm M của BC => M , I , K thg hàng
Bạn thùy dung chưa đọc kĩ đề bài ' đoạn BD mà '