Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E O H
Cm: a) Xét t/giác ABE và t/giác ACD
có: AB = AC (gt)
\(\widehat{A}\) :chung
AE = AD (gt)
=> t/giác ABE = t/giác ACD (c.g.c)
=> BE = CD (2 cạnh t/ứng)
b)Ta có: AD + DB = AB
AE + EC = AC
mà AD = AE (gt) ; AB = AC (gt)
=> BD = EC
Ta lại có: \(\widehat{ADC}+\widehat{CDB}=180^0\) (kề bù)
\(\widehat{AEB}+\widehat{BEC}=180^0\)(kề bù)
mà \(\widehat{ADC}=\widehat{AEB}\)(vì t/giác ABE = t/giác ACD)
=> \(\widehat{BDC}=\widehat{BEC}\)
Xét t/giác BOD và t/giác COE
có: \(\widehat{DBO}=\widehat{OCE}\) (vì t/giác ABE = t/giác ACD)
BD = EC (cmt)
\(\widehat{BDO}=\widehat{OEC}\) (cmt)
=> t/giác BOD = t/giác COE (g.c.g)
c) Xét t/giác ABO và t/giác ACO
có: AB = AC (gT)
OB = OC (vì t/giác BOD = t/giác COE)
AO : chung
=> t/giác ABO = t/giác ACO (c.c.c)
=> \(\widehat{BAO}=\widehat{CAO}\) (2 góc t/ứng)
=> AO là tia p/giác của \(\widehat{A}\)
d) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH : chung
=> t/giác ABH = t/giác ACH (c.g.c)
=> \(\widehat{BHA}=\widehat{CHA}\) (2 góc t/ứng)
Mà \(\widehat{BHA}+\widehat{CHA}=180^0\) (kề bù)
=> \(\widehat{BHA}=\widehat{CHA}=90^0\) => AH \(\perp\)BC (Đpcm)

a) ta có : AB=AC
Suy ra tam giac ABC cân
Xét tam giac ABE và tam giác ADE ta có
AB=AC(gt)
góc B=gócC(tính chất tam giác cân)
AD=AE(gt)
Suy ra tam giác ABE=tam giac ACD( c.g.c)
Suy ra BE=CD( hai cạnh tương ứng )
b) Ta có O nằm trên cạnh DC và BE
Suy ra DO=EO( DC=BE)
XÉT tam giác ADO và tam giác AEO ta có
AD=AE(gt)
AOchung
DO=EO( chứng minh trên)
Suy ra tam giác AOD = tam giác AEO(c.c.c)
Suy ra góc A1=A2 ( 2 góc tương ứng)
Suy ra AOlà tia phân giác của góc A

a.Xét tam giác DBC và tam giác ECB có:
DB=EC (AB=AC và AD=AE)
góc ABC = góc ACB (cân tại A)
BC là cạnh chung
Do đó tam giác DBC = tam giác ECB (c.g.c)
Suy ra BE= CD (ĐPCM)

a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD

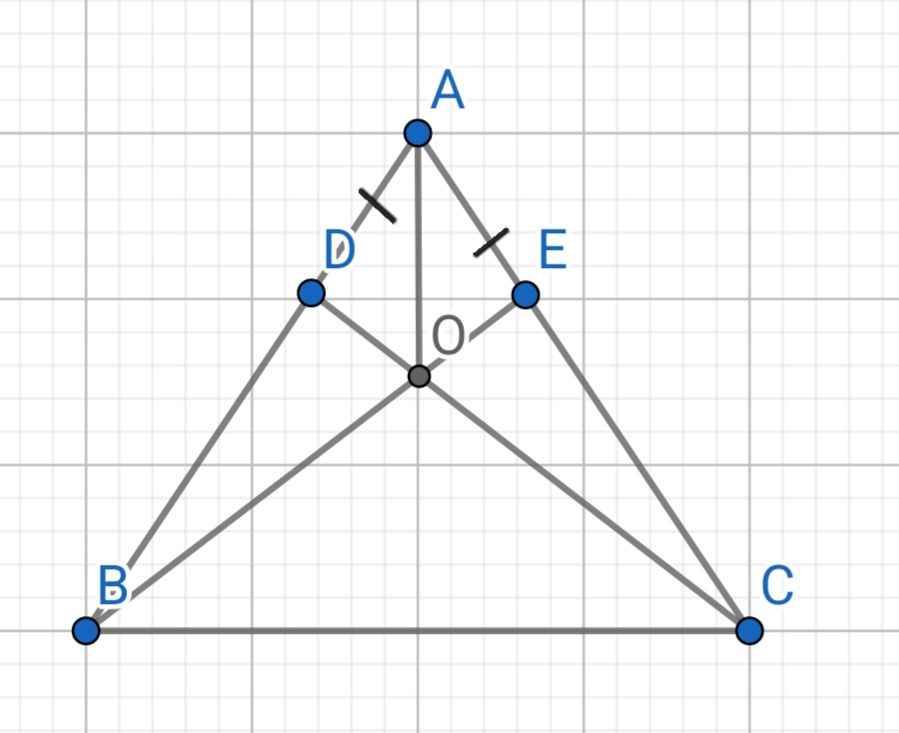 ∆ABC có:
∆ABC có:
AB = AC (gt)
⇒ ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
⇒ ∠DBC = ∠ECB
Do AB = AC (gt)
AD = AE (gt)
⇒ BD = AB - AD = AC - AE = CE
Xét ∆DBC và ∆ECB có:
DB = EC (cmt)
∠DBC = ∠ECB (cmt)
BC là cạnh chung
⇒ ∆DBC = ∆ECB (c-g-c)
⇒ ∠BDC = ∠CEB (hai góc tương ứng)
⇒ ∠BDO = ∠CEO
Do ∆DBC = ∆ECB (cmt)
⇒ ∠BCD = ∠CBE (hai góc tương ứng)
Mà ∠ACB = ∠ABC (cmt)
⇒ ∠ECO = ∠ACB - ∠BCD
= ∠ABC - ∠CBE
= ∠DBO
Xét ∆BOD và ∆COE có:
∠DBO = ∠ECO (cmt)
BD = CE (cmt)
∠BDO = ∠CEO (cmt)
⇒ ∆BOD = ∆COE (g-c-g)
⇒ OD = OE (hai cạnh tương ứng)
Xét ∆ADO và ∆AEO có:
AD = AE (gt)
AO là cạnh chung
OD = OE (cmt)
∆ADO = ∆AEO (c-c-c)
⇒ ∠DAO = ∠EAO (hai góc tương ứng)
⇒ AO là tia phân giác của ∠DAE
Hay AO là tia phân giác của ∠BAC
a: Xét ΔABE và ΔACD có
AB=AC
\(\stackrel\frown{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD