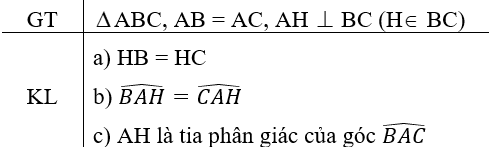
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

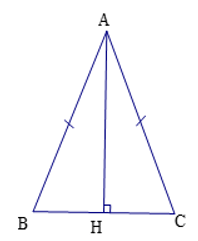
A B C D E H
a, Xét \(\Delta ABH\) và\(\Delta ACH\) CÓ:
\(AHchung\)
AB = AC
\(\widehat{AHB}=\widehat{AHC}\)
\(\Rightarrow\Delta ABH=\Delta ACH\)(cạnh huyền cạnh góc vuông)
=> BH = HC ( 2 cạnh tương ứng )
b,Do BC = 8cm => BH = 4cm
Áp dụng định lý Py ta go vào tam giác vuông ABH có :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH^2=AB^2-BH^2\)\(\Rightarrow AH^2=5^2-4^2=25-16=9\)\(\Rightarrow AH=3\left(cm\right)\)
c,\(Xét\Delta DBH\) và\(\Delta ECH\) có :
\(\widehat{ABH}=\widehat{ACH}\)
BH = HC
\(\widehat{BDH}=\widehat{CEH}\)
\(\Rightarrow\Delta DBH=\Delta ECH\)\(\Rightarrow DH=EH\)=> \(\Delta DHE\) cân tại H
cho mình 1 tym nha

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: BH=CH=12/2=6cm
=>AC=căn AH^2+HC^2=10cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H

a.ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến => HB = HC
b.áp dụng định lý pitago ta có:
\(AB^2=AH^2+HB^2\)
\(5^2=AH^2+\left(8:2\right)^2\)
\(AH=\sqrt{5^2-4^2}=3cm\)
c.Xét tam giác vuông BHD và tam giác vuông CHE, có:
BH = CH ( cmt )
góc B = góc C ( ABC cân )
Vậy tam giác vuông BHD = tam giác vuông CHE
=> HD = HE
=> HDE cân tại H
d.ta có AB = AD + DB
AC = AE + EC
Mà BD = CE ( 2 cạnh tương ứng của 2 tam giác bằng nhau )
=> AD = AE
=> ADE cân tại A
Mà A là đường cao cũng là đường trung trực trong tam giác cân ABC cũng là đường trung trực của tam giác cân ADE ( cmx )
Chúc bạn học tốt !!!!

Câu c. lên lớp 8 thì em có thể dùng đường trung bình dễ hơn nhiều nhé.

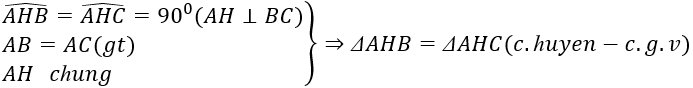
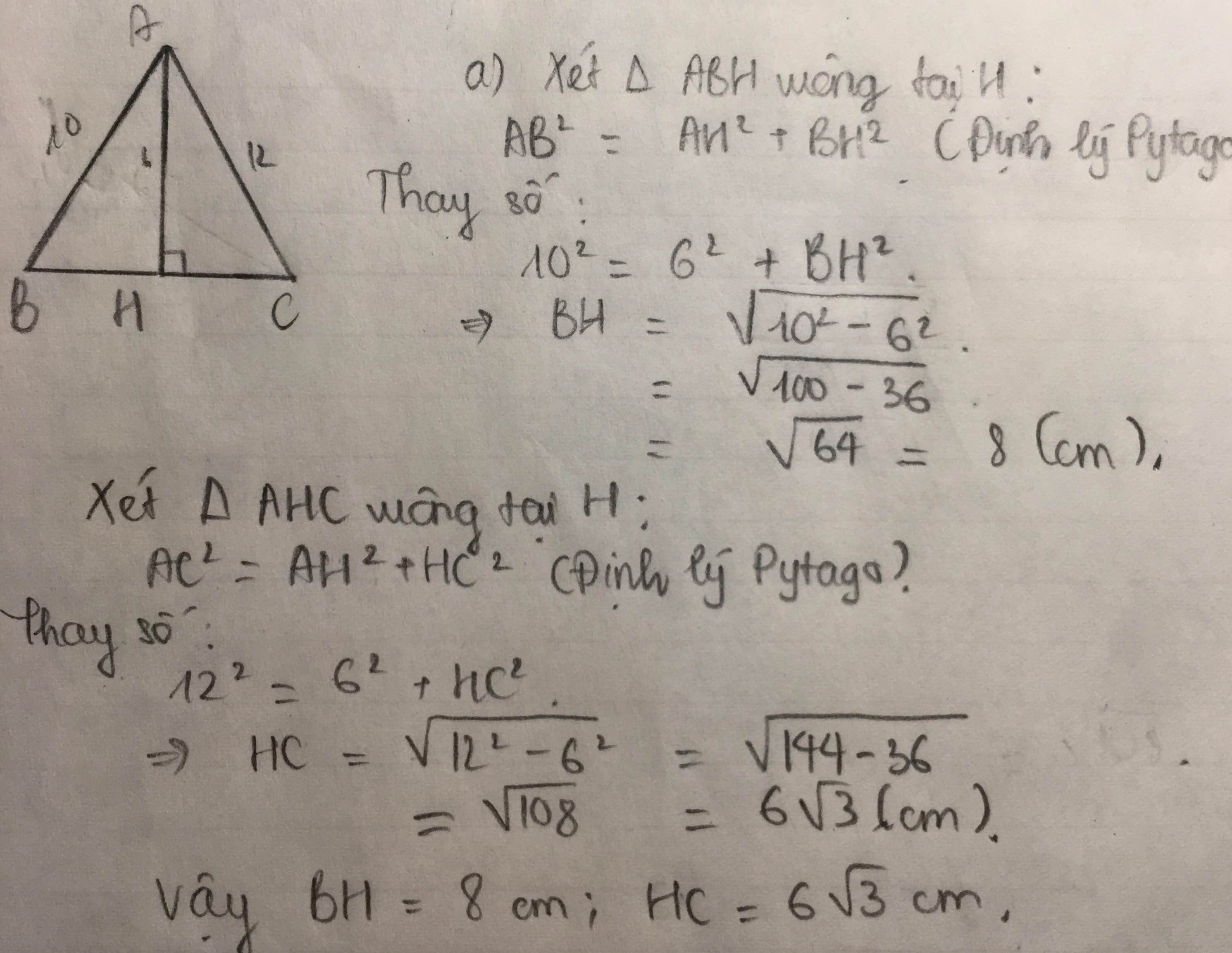
a) Xét ΔAHC vuông tại H và ΔBHC vuông tại H có
CA=CB(ΔABC cân tại C)
CH là cạnh chung
Do đó: ΔAHC=ΔBHC(cạnh huyền-cạnh góc vuông)
⇒HA=HB(hai cạnh tương ứng)
Ta có: ΔAHC=ΔBHC(cmt)
⇒\(\widehat{ACH}=\widehat{BCH}\)(hai góc tương ứng)
mà tia CH nằm giữa hai tia CA,CB
nên CH là tia phân giác của \(\widehat{ACB}\)(đpcm)
b) Ta có: AH+BH=AB(H nằm giữa A và B)
mà AH=BH(cmt)
nên \(AH=\frac{AB}{2}=\frac{12}{2}=6cm\)
Áp dụng định lí pytago vào ΔAHC vuông tại H, ta được
\(AC^2=AH^2+CH^2\)
hay \(CH^2=AC^2-AH^2=10^2-6^2=64\)
⇒\(CH=\sqrt{64}=8cm\)
Vậy: AH=6cm; CH=8cm