Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác vuông AMB và tam giác vuông AMC, có:
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
Vậy tam giác vuông AMB = tam giác vuông AMC ( cạnh huyền.góc nhọn)
b. Áp dụng định lý pitago vào tam giác vuông ABM, có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow BM=\sqrt{AB^2-AM^2}=\sqrt{15^2-12^2}=\sqrt{81}=9cm\)
c. Xét tam giác vuông AHM và tam giác vuông AKM, có:
góc HAM = góc KAM ( AH là đường cao cũng là đường phân giác )
AM: cạnh chung
Vậy tam giác vuông AHM = tam giác vuông AKM ( cạnh huyền.góc nhọn )
=> AH = AK ( 2 cạnh tương ứng ) (*)
d.(*) suy ra tam giác AHK cân tại A
Mà AM là đường phân giác => AM cũng là đường cao (1)
AM vuông với BC ( gt ) (2)
Từ (1) và (2) suy ra HK//BC

a) Xét 2 tam giác vuông: AMB và AMC có:
AM: cạnh chung
AB = AC (gt)
suy ra: tam giác AMB = tam giác AMC (ch-cgv)
b) Tam giác AMB = tam giácAMC
suy ra: góc BAM = góc CAM
Xét 2 tam giác vuông: AMH và AMK có:
AM: chung
góc HAM = góc
suy ra tam giác AMH = tam giác AMK
suy ra AH = AK

a, xét tam giác AMB và tam giác AMC có:
AB=AC(gt)
\(\widehat{BAM}\) =\(\widehat{CAM}\)(gt)
AM chung
suy ra tam giác AMB= tam giác AMC(c.g.c)
b,xét tam giác AHM và tam giác AKM có:
AM cạnh chung
\(\widehat{HAM}\)=\(\widehat{KAM}\)(gt)
suy ra tam giác AHM=tam giác AKM(CH-GN)
Suy ra AH=AK
c,gọi I là giao điểm của AM và HK
xét tam giác AIH và tam giác AIK có:
AH=AK(theo câu b)
\(\widehat{IAH}\)=\(\widehat{IAK}\)(gt)
AI chung
suy ra tam giác AIH=tam giác AIK (c.g.c)
Suy ra \(\widehat{AIH}\)=\(\widehat{AIK}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AIH}\)=\(\widehat{AIK}\)= 90 độ
\(\Rightarrow\)HK vuông góc vs AM

A B C M 1 2
a) Xét tam giác AMB và AMC có:
AM chung
AB=AC (tam giác ABC cân tại A)
\(\widehat{A_1}=\widehat{A_2}\)(AM là phân giác)
=> \(\Delta AMB=\Delta AMC\left(cgc\right)\)(đpcm)
b) Có tam giác ABC cân tại A (gt); AM là trung tuyến tam giác ABC
Vì trong tam giác cân đường trung tuyến trùng với đường cao
=> AM là đường cao tam giác ABC
=> AM _|_ BC (đpcm)
Bài làm
a) Xét tam giác AMB và tam giác AMC có:
^MAB = ^MAC ( Do AM phân giác )
AB = AC ( Do ∆ABC cân )
^B = ^C ( Do ∆ABC cân )
=> ∆AMB = ∆AMC ( g.c.g )
b) Cách 1: Vì ∆AMB = ∆AMC ( cmt )
=> ^AMB = ^AMC
Mà ^AMB + ^AMC = 180° ( hai góc kề bù )
=> ^AMB = ^AMC = 180°/2 = 90°
=. AM vuông góc với BC.
Cách 2: Vì tam giác ABC cân tại A
Mà AM là tia phân giác
=> AM đồng thời là đường cao.
=> AM vuông góc với BC .
c) Vì ∆ABC cân tại A
Mà AM vừa là đường phân giác, vừa là đường cao.
=> AM là đường trung tuyến.
=> BM = MC
Mà BM + MC = BC = 6
=> BM = MC = 6/2 = 3 ( cm )
Xét tam giác AMB vuông tại M có:
Theo định lí Pytago có:
AB² = AM² + BM²
=> AM² = AB² - BM²
Hay AM² = 5² - 3²
=> AM² = 25 - 9
=> AM² = 16
=> AM = 4 ( cm )
d) Xét tam giác ABC có:
AM vuông góc với BC
AH vuông góc với AC
Mà AM cắt AH tại H
=> H là trực tâm.
=> CH vuông góc với AB . ( Đpcm )

mk ko biết xin lỗi bạn nha!!!
mk ko biết xin lỗi bạn nha!!!
mk ko biết xin lỗi bạn nha!!!
mk ko biết xin lỗi bạn nha!!!

K
Hình hơi xấu hì hì! tự viết GT KL nha!
Cm:
a) \(\Delta ABC\)cân tại A (gt)
=> AB=AC
=>AC=4cm (vì AB=4cm(gt))
Vậy AC=4cm.
b) \(\Delta ABC\)cân tại A (gt)
=>\(\widehat{B}=\widehat{C}\)
\(\Delta ABC\)có:\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(ĐL tổng 3 góc trong 1 tam giác)
\(\Rightarrow60^0+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{B}=\widehat{C}=60^0\)
=> \(\Delta ABC\)đều.
c) Xét \(\Delta ABM\)và \(\Delta ACM\)có:
AM chung
AB=AC
BM=CM
=>\(\Delta ABM\)=\(\Delta ACM\) (c.c.c)
(đpcm)
d) Vì \(\Delta ABM\)=\(\Delta ACM\)(cmt)
=>\(\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(2 góc kề bù)
=>\(\widehat{AMB}=\widehat{AMC}=90^0\)
=> \(AM⊥BC\)(Đpcm)
e)Xét \(\Delta BHM\)và \(\Delta CKM\)có:
\(\widehat{BHM}=\widehat{CKM}=90^0\)
BM=CM
\(\widehat{B}=\widehat{C}\)
=>\(\Delta BHM\)=\(\Delta CKM\)(cạnh huyền-góc nhọn)
=>MH=MK(2 cạnh t/ứ)
(đpcm)

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
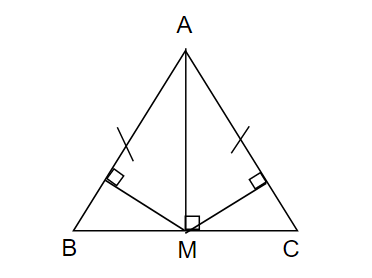
a: Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔABM vuông tại M có \(AB^2=MB^2+AM^2\)
hay MB=9(cm)
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: AH=AK
d: Xét ΔABC có AH/AB=AK/AC
nên HK//BC