Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF

a: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
góc FBC=góc ECB
Do đó: ΔFBC=ΔECB
=>CF=EB
b: Xét ΔMBC có góc MBC=góc MCB
nên ΔMCB cân tại M
=>MB=MC
mà AB=AC
nên AM là trung trực của BC

a) Tam giác ABE ( góc E=90 độ) và Tam giác ACF ( góc F=90 độ), có:
AB = AC ( gt )
Góc A chung
=> tam giác ... = tam giac ... ( cạnh huyền - góc nhọn)
=> BE = CF và góc ABE = góc ACF
b) Tam giác FCB ( góc F = 90 độ) và tam giác BEC ( góc E=90 độ), có:
BC chung
FC = EB ( c/m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> FB=EC
Tam giác ECI và tam giác FBI, có:
EC=FB (c/m trên)
góc E= góc F (=90 độ)
góc ACF = góc ABE (c/m trên)
=> tam giác ...= tam giác... (g-c-g)
c) Ta có: FA=AB - FB
EA=AC - EC
mà AB=AC; FB=EC
=> FA=EA
tam giác AIF(F=90 độ) tam giác AIE (E = 90 độ), có:
AI chung
FA=EA (c/ m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> góc BAI = góc CAI
hay AI là phân giác của góc A

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
FC=EB
Do đó: ΔFBC=ΔECB
Suy ra: \(\widehat{FCB}=\widehat{EBC}\)
=>ΔIBC cân tại I

1) Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC(ΔABC cân tại A)
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF(cạnh huyền-góc nhọn)
Suy ra: BE=CF(hai cạnh tương ứng)
Ta có: ΔABE=ΔACF(cmt)
nên \(\widehat{ABE}=\widehat{ACF}\)(hai góc tương ứng)
2) Ta có: ΔABE=ΔACF(cmt)
nên AE=AF(Hai cạnh tương ứng)
Ta có: AF+FB=AB(F nằm giữa A và B)
AE+EC=AC(E nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và AE=AF(cmt)
nên FB=EC
Ta có: \(\widehat{ABE}=\widehat{ACF}\)(cmt)
nên \(\widehat{FBI}=\widehat{ECI}\)
Xét ΔFBI vuông tại F và ΔECI vuông tại E có
FB=EC(cmt)
\(\widehat{FBI}=\widehat{ECI}\)(cmt)
Do đó: ΔFBI=ΔECI(cạnh góc vuông-góc nhọn kề)
Suy ra: IB=IC(hai cạnh tương ứng)
3) Xét ΔABI và ΔACI có
AB=AC(ΔABC cân tại A)
AI chung
IB=IC(cmt)
Do đó: ΔABI=ΔACI(c-c-c)
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)(hai góc tương ứng)
mà tia AI nằm giữa hai tia AB,AC
nên AI là tia phân giác của \(\widehat{BAC}\)(đpcm)
a) Tam giác ABE ( góc E=90 độ) và Tam giác ACF ( góc F=90 độ), có:
AB = AC ( gt )
Góc A chung
=> tam giác ... = tam giac ... ( cạnh huyền - góc nhọn)
=> BE = CF và góc ABE = góc ACF
b) Tam giác FCB ( góc F = 90 độ) và tam giác BEC ( góc E=90 độ), có:
BC chung
FC = EB ( c/m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> FB=EC
Tam giác ECI và tam giác FBI, có:
EC=FB (c/m trên)
góc E= góc F (=90 độ)
góc ACF = góc ABE (c/m trên)
=> tam giác ...= tam giác... (g-c-g)
c) Ta có: FA=AB - FB
EA=AC - EC
mà AB=AC; FB=EC
=> FA=EA
tam giác AIF(F=90 độ) tam giác AIE (E = 90 độ), có:
AI chung
FA=EA (c/ m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> góc BAI = góc CAI
hay AI là phân giác của góc A
chúc bạn học tốt nha :>

Vì tam giác ABC cân tại A
=> góc ABC= góc ACB ( 2 góc ở đáy)
Xét tam giác FBC vuông tại F và tam giác ECB vuông tại E có:
BC là cạnh chung
Góc ABC = góc ACB (cmt)
Suy ra Tam giác FBC=tam giác ECB ( c.h-g.n)
=> CF= BE ( 2 cạnh tương ứng)
Vậy BE=CF (đpcm)
A B C F E
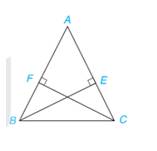
Do tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB}\)(tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
\(\widehat {ABC} = \widehat {ACB}\)
BC chung
=>\(\Delta BFC = \Delta CEB\)(cạnh huyền – góc nhọn)
=>\(CF=BE\) (2 cạnh tương ứng).