Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

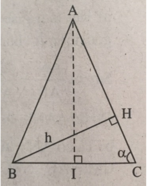
∠ A = 180 ° - 2 α . Tam giác vuông HBC có BC = h/sinα. Kẻ đường cao AI của tam giác ABC thì được
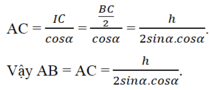

SABC=SADB+SADCSABC=SADB+SADC
<=>bc.sinA=AD⋅c⋅sinA2+AD⋅b⋅sinA2bc.sinA=AD⋅c⋅sinA2+AD⋅b⋅sinA2
<=>bc.sinA=AD⋅sinA2(b+c)bc.sinA=AD⋅sinA2(b+c)
<=>bc.sin2α=AD⋅sinα(b+c)bc.sin2α=AD⋅sinα(b+c)
<=>2bc.sinα.cosα=AD⋅sinα(b+c)2bc.sinα.cosα=AD⋅sinα(b+c)
<=>AD=2bc⋅cosαb+cAD=2bc⋅cosαb+c (dpcm)
a) Xét tam giác HAB và tam giác ABC có:
Góc AHB= góc BAC (= 900 )
B> là góc chung
⇒ tam giác HAB ~ tam giác ABC (g.g)
b) Xét ΔΔ ABC vuông tại A: BC2 = AB2 + AC2
Hay BC2 = 122 + 162
BC2 = 144 + 256 = 400
=> BC = √400 = 20 (cm)
Ta có : Δ HAB ∼ Δ ABC
=> HAAB=ABBCHAAB=ABBC
Hay HA12=1220HA12=1220
=> AH = 12.1220=7,212.1220=7,2 cm
c)
Ta có
DE là tia phân giác của góc ADB trong tam giác DAB,
áp dụng t/c tia phân giác thìDADB=AEEBDADB=AEEB
DG là tia phân giác cảu góc CDA trong tam giác CDA.
áp dụng t/c tia phân giác thì CDDA=CFFACDDA=CFFA
VẬy EAEB.DBDC.FCFA=DADB.DBDC.CDDA=1EAEB.DBDC.FCFA=DADB.DBDC.CDDA=1(dpcm)

A B D C
\(S_{ABC}=S_{ADB}+S_{ADC}\)
<=>\(bc.sinA=AD\cdot c\cdot sin\dfrac{A}{2}+AD\cdot b\cdot sin\dfrac{A}{2}\)
<=>\(bc.sinA=AD\cdot sin\dfrac{A}{2}\left(b+c\right)\)
<=>\(bc.sin2\alpha=AD\cdot sin\alpha\left(b+c\right)\)
<=>\(2bc.sin\alpha.cos\alpha=AD\cdot sin\alpha\left(b+c\right)\)
<=>\(AD=\dfrac{2bc\cdot cos\alpha}{b+c}\) (dpcm)

a) EF là đường trung bình của tam giác ABH => EF//AB; EF=1/2AB (1)
Có G là trung điểm của DC => GC//AB(DC//AB); GC=1/2AB(DC=AB) (2)
Từ (1)$(2) => EF//GC; EF=GC => Tứ giác EFCG là hình bình hành.
b) Xét tam giác EBH và tam giác CBH có:BH là cạnh chung
EHB=CHB=90 (gt)
EH=EC(H là trung điểm của EC)
Vậy tam giác EBH=tam giac CBH (cgv-cgv)
=>BEH=BCH ; EBH=CBH
Lại có:BEH+EBH+BCH+CBH=180 =>BEH=EBH=BCH=CBH=180/4=45 (3)
Co BCE+ECG=BCG
Ma BCG=90(ABCD là hcn); BCE=45(cmt)
=> ECG=45
Xét tam giác EGC có:EGC+GEC+ECG=180
=> EGC=180-(GEC+ECG)
=180-(90+45)=45 (4)
Tu (3)$(4) => BEG=90
c)Tu CM