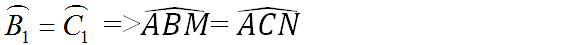Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1
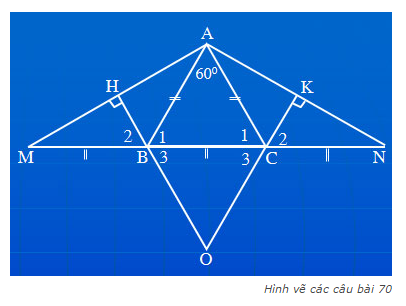
a) trước tiên chứng minh\(\widehat{ABM}=\widehat{ACN}\)
rồi mới chứng minh 2 tam giác ABM và ACN bằng nhau
suy ra AM = AN
b)Đầu tiên chứng minh\(\widehat{ABH}=\widehat{ACK}\)
rồi chứng minh hai tam giác ABH và ACK bằng nhau
suy ra BH = CK
c) vì hai tam giác ABH và ACK bằng nhau (cmt)
nên AH = AK
d) ta có \(\widehat{AMB}=\widehat{ACN}\)(hai tam giác ABH và ACK bằng nhau)
nên dễ cm \(\widehat{MBH}=\widehat{NCK}\)
còn lại tự cm
e) dễ cm tam giác ABC đều
vẽ \(BH\perp AC\)
nên BH vừa là đường cao; phân giác và trung tuyến
dễ cm \(\Delta BHC=\Delta NKC\)
nên \(\widehat{BCH}=\widehat{NCK}=60^0\)
từ đó dễ cm AMN cân và OBC dều

a) xét \(\Delta MBE\)vuông tại E và \(\Delta HBE\)
có \(EM=EH\left(gt\right)\)
BE là cạnh chung
\(\Rightarrow\Delta MBE=\Delta HBE\left(ch-cgv\right)\)
\(\Rightarrow\widehat{MBE}=\widehat{HBE}\)( 2 góc tương ứng)
xét \(\Delta MAE\)VUÔNG TẠI E và \(\Delta HAE\)VUÔNG TẠI E
CÓ EM=EH (gt)
AE LÀ CẠNH CHUNG
\(\Rightarrow\Delta MAE=\Delta HAE\left(ch-cgv\right)\)
\(\Rightarrow\widehat{MAE}=\widehat{HAE}\)(2 GÓC TƯƠNG ỨNG)
XÉT \(\Delta ABM\)VÀ \(\Delta ABH\)
CÓ \(\widehat{MBE}=\widehat{HBE}\left(cmt\right)\)
AB LÀ CẠNH CHUNG
\(\widehat{MAE}=\widehat{HAE}\left(cmt\right)\)
\(\Rightarrow\Delta ABM=\Delta ABH\left(g-c-g\right)\)
MÀ TAM GIÁC ABH VUÔNG TẠI H
=> TAM GIÁC ABM VUÔNG TẠI M
=> \(AM\perp BM\)( ĐỊNH LÍ)
B) TA CÓ \(AC\perp AB\)
\(HE\perp AB\)
\(\Rightarrow AC//HE\)(ĐỊNH LÍ)
\(\Rightarrow\widehat{EHA}=\widehat{HAF}\left(SLT\right)\)
XÉT \(\Delta EHA\)VUÔNG TẠI E VÀ \(\Delta FAH\)VUÔNG TẠI F
CÓ \(\widehat{EHA}=\widehat{HAF}\left(cmt\right)\)
HA LÀ CẠNH CHUNG
\(\Rightarrow\Delta EHA=\Delta FAH\left(ch-gn\right)\)
=> EA = FH (2 CẠNH TƯƠNG ỨNG)
XÉT \(\Delta EAH\)VUÔNG TẠI E VÀ \(\Delta HFE\)VUÔNG TẠI H
CÓ EA= FH (cmt)
EH LÀ CẠNH CHUNG
\(\Rightarrow\Delta EAH=\Delta HFE\left(cgv-cgv\right)\)
=> AH = EF (2 CẠNH TƯƠNG ỨNG)
CHÚC BN HỌC TỐT!!!!!!!!!!

Câu 1:
Xét tam giác AMB và tam giác AMC ta có:
AB = AC (tam giác ABC cân tại A)
ABM = ACM (tam giác ABC cân tại A)
=> Tam giác AMB = tam giác AMC (ch-gn) (dpcm)
Câu 2:
a) Ta có: +) AK+KB = AB => KB = AB-AK
+) AH+HC = AC => HC = AC-AH
Mà AB=AC(tam giác ABC cân tại A) ; AK=AH (gt)
=>KB=HC
Xét tam giác BHC và tam giác CKB ta có:
HC=KB (cmt)
HCB=KBC (tam giác ABC cân tại A)
BC là cạnh chung
=>tam giác BHC = tam giác CKB (c.g.c)
=>BH=CK (2 cạnh tương ứng) (dpcm)
Xét tam giác ABH và tam giác ACK ta có:
AB=AC (tam giác ABC cân tại A)
BH=CK (cmt)
AH=AK (gt)
=> tam giác ABH = tam giác ACK (c.c.c)
=> ABH = ACK (2 góc tương ứng) (dpcm)
b) Theo a) tam giác BHC= tam giác CKB
=> HBC=KCB (2 góc tương ứng) hay OBC=OCB
=> Tam giác OBC là tam giác cân tại O (dpcm)
c) Theo b tam giác OBC cân tại O => OB=OC
Theo a góc ABH = góc ACK => KBO= HCO
Xét tam giác OKB và tam giác OHC ta có:
KB=HC (theo a)
KBO=HCO (cmt)
OB=OC (cmt)
=> tam giác OKB = tam giác OHC (c.g.c)
=> OK = OH (2 cạnh tương ứng) hay tam giác OKH là tam giác cân tại O (dpcm)
d) Gọi giao điểm của AO và KH là I
Xét tam giác AKO và tam giác AHO ta có:
AK=AH (gt)
AO là cạnh chung
OK=OH (theo c)
=> tam giác AKO = tam giác AHO (c.c.c)
=> KAO = HAO (2 góc tương ứng) hay KAI=HAI
Xét tam giác KAI và tam giác HAI ta có:
AK=AH (gt)
KAI=HAI (cmt)
AI là cạnh chung
=> tam giác KAI = tam giác HAI ( c.g.c)
=> KI=HI , mà I nằm giữa H và K
=> I là trung điểm của KH hay
AO đi qua trung điểm của KH (dpcm)

A B C D K E H
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^o\) (kề bù)
\(\widehat{ACB}+\widehat{ACE}=180^o\)(kề bù)
Mà \(\widehat{ABC}=\widehat{ACB}\) (do \(\Delta ABC\) cân tại A)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét hai tam giác ABD và ACE có:
\(\widehat{BAD}=\widehat{CAE}\) (gt)
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
Vậy: \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)
Suy ra: BD = CE (hai cạnh tương ứng)
b) Xét hai tam giác BHD và CKE có:
BD = CE (cmt)
\(\widehat{ADB}=\widehat{AEC}\) (\(\Delta ABD=\Delta ACE\))
Vậy: \(\Delta BHD=\Delta CKE\left(ch-gn\right)\)
Suy ra: BH = CK (hai cạnh tương ứng).

MK cần bạn vẽ hình để giải được câu b và c nhé
Ta có AB vuông AC; EK vuông AC Nên AB song song với EK
=> goc BAE= goc AEK (1) ( hai góc so le trong)
Lại có góc BAE= góc BEA (2) ( do tam giác ABM= tam giác EBM chứng minh ở câu a)
(1)(2)=> góc AEB = góc AEK
c.
Xét \(\Delta AEH\)và \(\Delta AEK\)
\(H=K\)
Chung \(AE\)
\(\Rightarrow\Delta AEH=\Delta AEK\left(ch-gn\right)\Rightarrow\hept{\begin{cases}AH=AK\\HAE=KAE\end{cases}}\)
Gọi giao điểm giữa HK và AE là N
Xét \(\Delta AHN\)và \(\Delta AKN\)
\(AH=AK\left(cmt\right)\)
\(HAN=KAN\left(cmt\right)\)
Chung \(AN\)
\(\Rightarrow\Delta AHN=\Delta AKN\left(c.g.c\right)\Rightarrow AMH=AMK\Rightarrow2AMH=AMK+AMH=180\Rightarrow AMH=90\)
Vậy \(AE\perp HK\)tại \(N\)

LƯU Ý: MÌNH KHÔNG BIẾT VẼ HÌNH NÊN BẠN VẼ NHÉ
Bài 1: DỰNG TAM GIÁC ĐỀU MBC ( M;A nằm trên cùng một nửa mặt phẳng bờ BC)
Xét tam giác MAB và tam giác MAC
MB=MC(tam giác MBC đều)
Chung MA
AB=AC(tam giác ABC cân tại A)
=> Tam giác MAB= tam giác MBC => góc BMA= góc CMA
=> góc BMA=30 độ
Xét tam giác BMA và tam giác BCD
góc BMA=BCD(=30)
BM=BC(tam giác MBC đều)
goc MBA=CBD(=10) (CHỖ NÀY BẠN KHÔNG HIỂU HỎI MK NHÉ )
=> tam giac BMA=BCD=>AB=DB=> tam giac BAD cân tại B . Lại có DBM=40
=> BAD=(180-40)/2=70
Bài 2: Dựng tam giác đều BCI( I;A cùng phía so với BC)
Xét tam giác BIA và tam giác CIA
AB=AC ( ABC cân tại A)
ABI=ACI(=10)
BI=CI(do BIC đều)
=> tam giác BIA=CIA =>góc BAI=CAI=40/2=20
Tương tự ta chứng minh được tam giác ABI = tam giác DBC(c.g.c) ( NẾU HỎI MK SẼ NHẮN TRONG PHÂN CHAT)
Do đó BAI=BDC hay BDC=20