Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) OBNC có NCO=OBN=90 nên OBNC là tứ giác nội tiếp
b) Xét tam giác ADC có AB,DC là các đường cao
mà AB cắt DC tại O
suy ra O là trực tâm của tam giác ADC
nên NO vuông góc với AD
c)
CONB là tứ giác nôi tiếp nên COA=CNB
Xét tam giác ACO và tam giác DCN
COA=CNB(cmt)
ACO=NCD=90
nên tam giác ACO đồng dạng với tam giác DNC
nên CA.CN=CO.CD
Còn câu d mk chịu

Câu a : Ta có : \(\Delta OMA\) cân tại O và \(AC=MC\) nên \(OC\perp AM\) hay \(\widehat{OCN}=90^0\) .
Xét tứ giác OBNC ta có :
\(\widehat{OCN}=90^0\) ( cmt )
\(\widehat{OBN}=90^0\) ( Tiếp tuyến vuông góc với bán kính )
\(\Rightarrow\widehat{OCN}+\widehat{OBN}=180^0\) hay OBNC là tứ giác nội tiếp (đpcm )
Câu b : Xét tam giác AND ta có :
AB là đường cao xuất phát từ đỉnh A .
DC là đường cao xuất phát từ đỉnh D .
Mà hai đường cao này cắt nhau tại O cho nên O là trực tâm của \(\Delta AND\)
NO cắt AD suy ra NO là đường cao của tam giác AND \(\Rightarrow NO\perp AD\)
Câu c : Ta có : \(\left\{{}\begin{matrix}\widehat{CAO}+\widehat{ANB}=90^0\\\widehat{CDN}+\widehat{ANB}=90^0\end{matrix}\right.\Rightarrow\widehat{CAO}=\widehat{CDN}\)
Xét tam giác CAO và tam giác CDN ta có :
\(\left\{{}\begin{matrix}\widehat{ACO}=\widehat{DCN}\left(=90^0\right)\\\widehat{CAO}=\widehat{CDB}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta CAO\sim\Delta CDN\left(g-g\right)\)
\(\Rightarrow\frac{CA}{CD}=\frac{CO}{CN}\Rightarrow CA.CN=CO.CD\) ( đpcm )
Câu d : Xét tam giác AMB và tam giác ABN ta có :
\(\left\{{}\begin{matrix}\widehat{BAM}:chung\\\widehat{AMB}=\widehat{ABN}\left(=90^0\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMB\sim\Delta ABN\left(g-g\right)\)
\(\Rightarrow\frac{AM}{AB}=\frac{AB}{AN}\Rightarrow AM.AN=AB^2=4R^2\)
Áp dụng BĐT Cô - si ta có : \(2AM+AN\ge2\sqrt{2AM.AN}=2\sqrt{8R^2}=4R\sqrt{2}\)
Vậy GTNN của 2AM + AN là \(4R\sqrt{2}\) khi và chỉ khi M là trung điểm của AN

super easy!
theo hệ thức lượng và BĐT cô-si:
\(MF+2ME\ge2\sqrt{2MF.ME}=2\sqrt{2MN^2}=2MN\sqrt{2}\)
Vậy GTNN của MF+2ME là \(2MN\sqrt{2}\)
Đẳng thức xảy ra \(\Leftrightarrow\) \(\hept{\begin{cases}MF=2ME\\MF+2ME=2MN\sqrt{2}\end{cases}}\)
\(\Rightarrow\) \(2MF=2MN\sqrt{2}\)
\(\Leftrightarrow MF=MN\sqrt{2}\)
Ta có \(\sin F=\frac{MN}{MF}=\frac{1}{\sqrt{2}}\) nên \(\widehat{F}=45^0\)
Hay tam giác MNF vuông cân => ... => tam giác MNE vuông cân => ME = NE => E nằm chính giữa cung MN
p/s: làm bài tốt ko bn?


4) Ta có: \(AM//PQ\)( cùng vuông góc với OC )
Xét tam giác COQ có: \(EM//OQ\)
\(\Rightarrow\frac{CE}{CO}=\frac{EM}{OQ}\)( hệ quả của định lý Ta-let ) (1)
Xét tam giác COP có: \(AE//OP\)
\(\Rightarrow\frac{CE}{CO}=\frac{AE}{OP}\)( hệ quả của định lý Ta-let ) (2)
Từ (1) và (2) \(\Rightarrow\frac{EM}{OQ}=\frac{AE}{OP}\)Mà AE=EM
\(\Rightarrow OQ=OP\)
Xét tam giác CPQ và tam giác COP có chung đường cao hạ từ C, đáy \(OP=\frac{PQ}{2}\)
\(\Rightarrow S_{\Delta CPQ}=2.S_{\Delta COP}\)
Ta có: \(S_{\Delta COP}=\frac{1}{2}OA.CP=\frac{1}{2}R.CP\)
Áp dụng hệ thức lượng trong tam giác COP vuông tại O có đường cao OA ta có:
\(OA^2=CA.AP\)
Mà \(CA.AP\le\frac{\left(CA+AP\right)^2}{4}=\frac{PC^2}{4}\)( BĐT cô-si )
Dấu "=" xảy ra \(\Leftrightarrow AC=AP\)
\(\Rightarrow PC^2\ge4OA^2\)
\(\Rightarrow PC\ge2OA=2R\)
\(\Rightarrow S_{\Delta COP}\ge R^2\)
\(\Rightarrow S_{\Delta CPQ}\ge2R^2\)
Dấu "=" xảy ra \(\Leftrightarrow AC=AP\)
Mà tam giác COP vuông tại O có đường cao OA
\(\Rightarrow AC=AP=OA=R\)
Khi đó áp dụng định lý Py-ta-go vào tam giác CAO vuông tại A ta được:
\(AC^2+AO^2=OC^2\)
\(\Rightarrow OC=\sqrt{AC^2+AO^2}=R\sqrt{2}\)
Vậy điểm C thuộc đường thẳng d sao cho \(OC=R\sqrt{2}\)thì diện tích tam giác CPQ nhỏ nhất

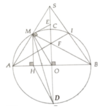
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC
