NQ
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
13 tháng 5 2017
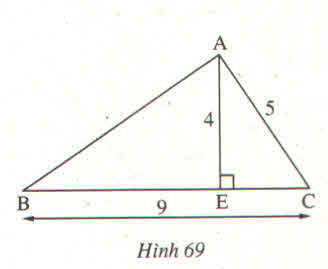
Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)
LT
12 tháng 5 2017
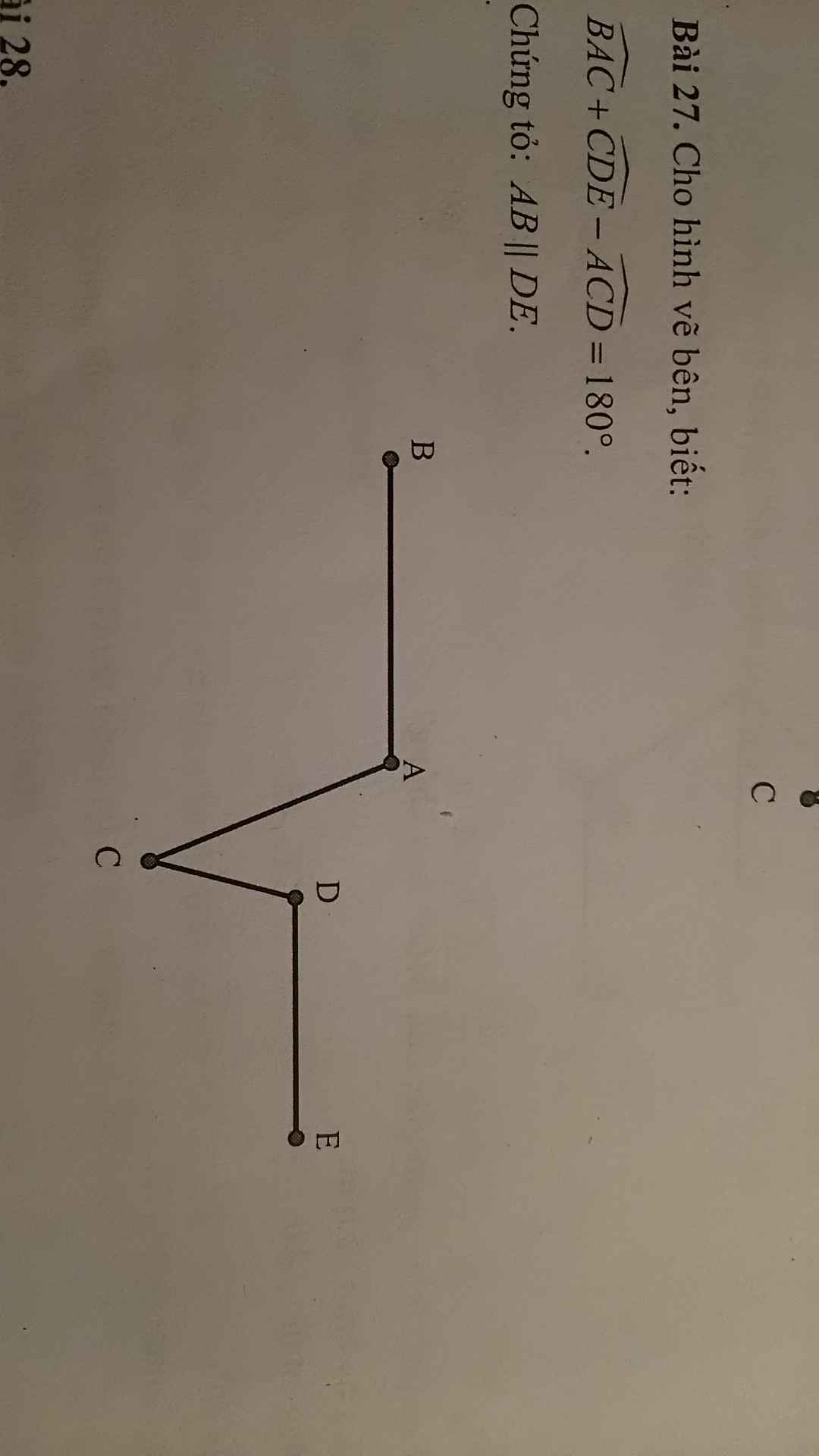
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD
SG
1
DN
20 tháng 4 2017
Ta có:
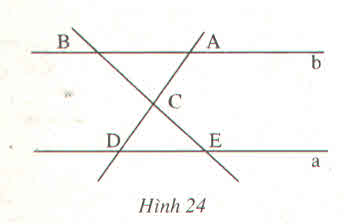
^ECD = ^ACB (2 góc đối đỉnh).
Vì a // b nên:
^ABC = ^CED và ^CDE = BAC (2 góc so le trong)
Vậy các cặp góc bằng nhau của 2 tam giác CAB và CDE là: ^ACB = ^ECD; ^BAC = ^CDE; ^ABC = ^CED.
27 tháng 5 2017
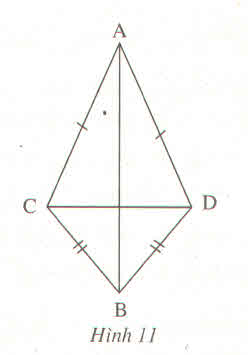
Ta có : AB=AC
=> \(\Delta ABC\) là tam giác vuông cân tại A ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{ABC}=A\widehat{CB}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{ABC}=A\widehat{CB}=45^0\)
=> \(\widehat{CBD}=\widehat{A}+\widehat{BCA}=135^0\) ( góc ngoài của tam giác )
Ta lại có:
BD=BC
=> \(\Delta BCD\) cân tại B ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{BDC}=\widehat{BCD}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{BDC}=\widehat{BCD}=\dfrac{\left(180^0-135^0\right)}{2}=\dfrac{45^0}{2}=22,5^0\)
Mà \(\widehat{ACD}=\widehat{BCA}+\widehat{BCD}\)
=> \(\widehat{ACD}=45^0+22,5^0=67,5^0\)
Vậy trong \(\Delta ACD\) có :
\(\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{ADC}=22,5^0\\\widehat{ACD}=67,5^0\end{matrix}\right.\)
SG
1
19 tháng 4 2017
a) Trong hình vẽ BE < BC là hai đường xiên vẽ từ B đến đường AC và AE, AC là hai hình chiếu của chúng vì AE < AC nên BE < BC
b) EB và ED là hai đường xiên vẽ từ E đến AB
AB và AD là hai hình chiếu của chúng
Vì AD < AB nên DE < BE
Ta có: BE < BC và DE < BE nên DE < BC
SG
1
18 tháng 7 2017
giải
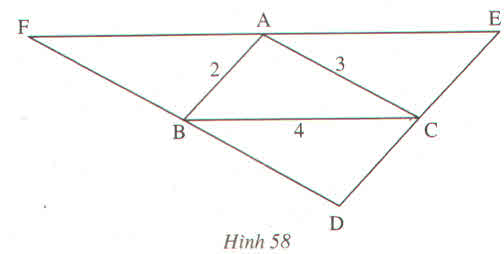
*xét tam giác abc và tam giác abf có
góc abc=góc bà(so le trong)
ad;chung
góc bac=góc abf(so le trong)
suy ra tam giác abc=tam giác abf(gcg)
suy ra af=bc=4(2 cạnh tương ứng)
bf=ac=3
*xét tam giác abc và tam giác ace có
góc acb=góc cae(số lẻ trong)
ac; chung
gốc bac= gốc eca(slt)
suy ra tam giác abc= tam giác ace
suy ra ae=bc=4(2 cạnh tương ứng)
ce=ab=2
* xét tam giác abc và tam giác dcb có
góc acb= góc dbc(slt)
bc;chung
góc abc= góc dcb
suy ra tam giác abc=tam giác dcb
suy ra dc=ab=2
db=ac=3
ta có ef=ae+af=4+4=8
df=db+bf=3+3=6
de=dc+ce=2+2=4
vậy chu vi của tam giác def là
để+DF+EF=4+6+8=18(ĐƠN VỊ ĐO ĐỘ DÀI)
SG
3
2 tháng 6 2017
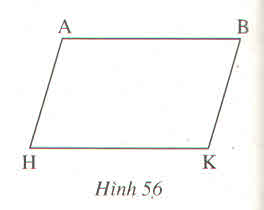
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
DT
1 tháng 12 2017
kẻ đoạn thẳng AK
Xét tamgiác KAH và tam giác AKB
góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )
cạnh AK chung
góc HKA = góc BAK (2 góc so le trong do AB //HK )
=> tam giác KAH = tam giác AKB ( g.c.g.)
=> AB=HK (2 cạnh tương ướng )
=> AH = BK (2 cạnh tương ướng )
đúng không..............................................
SG
4
19 tháng 4 2017
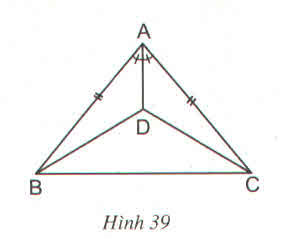
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
ˆBAD=ˆCADBAD^=CAD^
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> ˆDBC=ˆDCB
19 tháng 4 2017
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210
c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL