Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
Ta có:
\(p=x^4+2^{4n+2}=(x^2)^2+(2^{2n+1})^2=(x^2+2^{2n+1})^2-2.x^2.2^{2n+1}\)
\(=(x^2+2^{2n+1})^2-(x.2^{n+1})^2\)
\(=(x^2+2^{2n+1}+x.2^{n+1})(x^2+2^{2n+1}-x.2^{n+1})\)
Từ đây ta thấy để p là số nguyên tố thì bắt buộc một trong hai thừa số trên phải bằng một
Vì \(x^2+2^{2n+1}+x.2^{n+1}> x^2+2^{2n+1}-x.2^{n+1}\) nên
\(x^2+2^{2n+1}-x.2^{n+1}=1\)
\(\Leftrightarrow 2x^2+2^{2n+2}-2.x.2^{n+1}=2\)
\(\Leftrightarrow x^2+(x-2^{n+1})^2=2\)
\(\Rightarrow x^2=2-(x-2^{n+1})^2\leq 2\Rightarrow x\leq \sqrt{2}\)
\(\Rightarrow x\in\left\{0;1\right\}\)
Nếu \(x=0\): \(\Rightarrow 2^{2n+1}=1=2^0\Rightarrow 2n+1=0\) (vô lý với n là số tự nhiên)
Nếu \(x=1\Rightarrow 1+2^{2n+1}-2^{n+1}=1\)
\(\Leftrightarrow 2^{2n+1}-2^{n+1}=0\Leftrightarrow 2n+1=n+1\)
\(\Leftrightarrow n=0\)
Khi đó \(p=5\in \mathbb{P}\)
Vậy \((x,n)=(1;0)\)
Bài 3:
a)
\(p=x^4+x^2-6x+9\)
Áp dụng BĐT AM-GM cho các số không âm:
\(x^4+x^2+1+1+1+1\geq 6\sqrt[6]{x^6}=6|x|\geq 6x\)
\(\Leftrightarrow x^4+x^2+4\geq 6x\)
Suy ra \(p=(x^4+x^2+4)-6x+5\geq 6x-6x+5=5\)
Vậy \(p_{\min}=5\Leftrightarrow \left\{\begin{matrix} x^4=x^2=1\\ x\geq 0\end{matrix}\right.\Leftrightarrow x=1\)
b) Phản chứng
Giả sử \(n^2+11n+39\vdots 49\)
Khi đó suy ra \(n^2+11n+39\vdots 7\)
\(\Leftrightarrow n^2+11n+39-7n-35\vdots 7\)
\(\Leftrightarrow n^2+4n+4\vdots 7\)
\(\Leftrightarrow (n+2)^2\vdots 7\)
\(\Leftrightarrow n+2\vdots 7\) (do 7 là số nguyên tố)
Khi đó đặt \(n+2=7t\Rightarrow n^2+11n+39=(7t-2)^2+11(7t-2)+39\)
\(\Leftrightarrow n^2+11n+39=49t^2+49t+21\) không chia hết cho $49$
Điều này mâu thuẫn với điều ta đã giả sử.
Do đó điều giả sử là sai. Hay \(n^2+11n+39\not\vdots 49\)
Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD
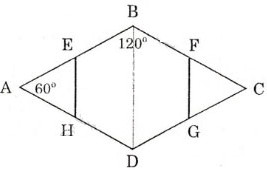
ABCD là hình thoi, 
= 
nên 
= 
, 
= .
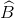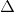EAH là tam giác đều (vì tam giác cân có một góc ) nên 
= , 
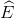= . Cũng thế 
= , 
= .
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
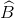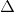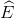ABCD là hình thoi, = nên = , = .EAH là tam giác đều (vì tam giác cân có một góc ) nên = , = . Cũng thế = , = .
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều
Hình tự vẽ nhé , với lại chỉ ghi hướng cho nhan thôi chứ làm chi tiết lâu lắm
a)Chứng minh AG vuông góc với HF ( để ý góc D = 60 đỏồi tính toán các góc để có được góc = 90 độ)
Gọi FG giao với BD tại M, thì dễ dàng chứng minh được M là trung điểm của FG => IM là đường trung bình
=> IM //AG
Mà AG vuông góc với HF => IM vuông góc với HF
gọi PG giao với MH=O, thì dễ dàng chứng minh PHGM là hình chữ nhật => O là trung điểm của PG và HM
thì ta có tam giác HIM vuông tại I có O là trung điểm của HM => IO=1/2HM=1/2PG => tam giác PIG vuông tại I(ĐPCM)
hóng các cao nhân ý b ^_^