Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân
Nguyễn Huy Tú1505GP
Ace Legona1252GP
soyeon_Tiểubàng giải850GP
Trần Việt Linh739GP
Hoàng Lê Bảo Ngọc688GP
Võ Đông Anh Tuấn657GP
Phương An650GP
Silver bullet592GP
Tuấn Anh Phan Nguyễn464GP
Hoàng Ngọc Anh
5)
a)
Có 3x+y = 1
\(\Rightarrow x+x+x+y=1\)
Áp dụng bất đẳng thức bunhiacopxki ta có :
\(\left(x^2+x^2+x^2+y^2\right)\left(1^2+1^2+1^2+1^2\right)\ge\left(x+x+x+y\right)^2\)
\(\Rightarrow3x^2+y^{2^{ }}.4\ge\left(3x+y\right)^2\)
\(\Rightarrow3x^2+y^2\ge\dfrac{1}{4}\)
b)
Áp dụng bất đẳng thức AM - GM ta có :
\(\left[{}\begin{matrix}a^2+1^2\ge2a\\b^2+1^2\ge2b\\c^2+1^2\ge2c\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(a+1\right)^2\ge4a^{ }\\\left(b+1\right)^2\ge4b^{ }\\\left(c+1\right)^2\ge4c^{ }\end{matrix}\right.\)
\(\Rightarrow\left(a+1\right)^2\left(b+1\right)^2\left(c+1\right)^2\ge4a^{ }.4b.4c^{ }\)
\(\Rightarrow\left(a+1\right)^2\left(b+1\right)^2\left(c+1\right)^2\ge64a^{ }bc^{ }\)
\(\Rightarrow\left(a+1\right)^2\left(b+1\right)^2\left(c+1\right)^2\ge64abc\)
\(\Rightarrow\left(a+1\right)^2\left(b+1\right)^2\left(c+1\right)^2\ge64\)
\(\Rightarrow\left(a+1\right)^{ }\left(b+1\right)^{ }\left(c+1\right)^{ }\ge8\) \(\left(đpcm\right)\)
3)
Sửa đề \(A=\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}\)
Đặt b + c - a = x , a+c-b = y , a+b-c= z
\(\Rightarrow\left[{}\begin{matrix}2a=y+z\\2b=x+z\\2c=x+y\end{matrix}\right.\)
Có :
\(\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}\)
\(\Rightarrow\dfrac{2a}{b+c-a}+\dfrac{2b}{a+c-b}+\dfrac{2c}{a+b-c}\)
\(\Rightarrow\dfrac{y+z}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}\)
\(\Rightarrow\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)\)
Áp dụng bất đẳng thức \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\forall a,b>0\)
\(\Rightarrow\) \(\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)\ge6\)
\(\Rightarrow\dfrac{2a}{b+c-a}+\dfrac{2b}{a+c-b}+\dfrac{2c}{a+b-c}\ge6\)
\(\Rightarrow2\left(\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}\right)\ge6\)
\(\Rightarrow\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}\ge3\) \(\left(đpcm\right)\)
\(\left(m-n\right)^6-6\left(m-n\right)^4+12\left(m-n\right)^2-8=\left[\left(m-n\right)^2-2\right]^3\)
\(\dfrac{8}{27}a^3-\dfrac{8}{3}a^2b+8b^2a-8b^3=\left(\dfrac{2}{3}a-2b\right)^3\)
Chúc bạn học tốt !!
a) Ta có \(x^2-6x+11=\left(x-3\right)^2+2\ge2;y^2+2y+4=\left(y+1\right)^2+3\ge3\)
=>\(\left(x^2-6x+11\right)\left(y^2+2y+4\right)\ge2.3=6\)
Mà \(4z-z^2+2=6-\left(z^2-4z+4\right)=6-\left(z-2\right)^2\le6\)
=>VT>=VP
Dấu = xảy ra tự tìm nhé ^^
3)
Ta có \(BĐT\Leftrightarrow a^4-4a+3\ge0\Leftrightarrow a^4-2a^2+1+2a^2-4a+1\ge0\)
\(\Leftrightarrow\left(a^2-1\right)^2+2\left(a^2-2a+1\right)\ge0\Leftrightarrow\left(a^2-1\right)^2+2\left(a-1\right)^2\ge0\left(lđ\right)\)
=> BĐt cần chứng minh luôn đúng
Dấu = xảy ra <=> a=1 nhé, có dấu = bạn nhé
^^
a, \(\frac{2x}{x+1}+\frac{18}{x^2+2x-3}=\frac{2x-5}{x+3}\)
\(\Leftrightarrow\frac{2x}{x+1}+\frac{18}{\left(x+3\right)\left(x-1\right)}=\frac{2x-5}{x+3}\)
\(\Leftrightarrow\frac{2x\left(x-1\right)\left(x+3\right)}{\left(x+1\right)\left(x-1\right)\left(x+3\right)}+\frac{18\left(x+1\right)}{\left(x+3\right)\left(x-1\right)\left(x+1\right)}=\frac{\left(2x-5\right)\left(x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x+3\right)\left(x+1\right)}\)
\(\Leftrightarrow2x\left(x-1\right)\left(x+3\right)+18\left(x+1\right)=\left(2x+5\right)\left(x+1\right)\left(x-1\right)\)
\(\Leftrightarrow2x^3+4x^2-6x+18x+18=2x^3-2x+5x^2-5\)
\(\Leftrightarrow-x^2+14x+23=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=7-6\sqrt{2}\\x=7+6\sqrt{2}\end{cases}}\)
Vậy...
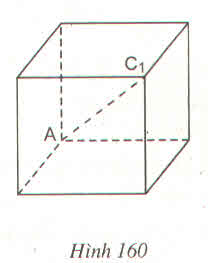
Hình lập phương đã cho gồm 6 mặt bằng nhau. Mỗi mặt là hình vuông có độ dài cạnh là 2cm
Diện tích mỗi mặt là: 2 2 = 4 c m 2
Tổng diện tích các mặt của hình lâp phương là: 4 . 6 = 24 c m 2
Chọn đáp án D