Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
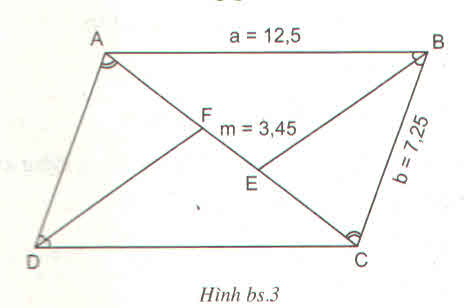
\(\widehat{ABC}=\widehat{ADC}\) và AD = BC = b = 7,25cm vì ABCD là hình bình hành.
Xét hai tam giác ADF và CBE ta có:
\(\widehat{ABC}=\widehat{ADC}\) (cmt)
AD = BC (cmt)
\(\widehat{DAF}=\widehat{BCE}\) (2 góc so le trong)
Vậy \(\Delta ADF=\Delta CBE\) (g-c-g).
=> AF = CE.
Cho AF = CE = x.
Áp dụng tính chất của đường phân giác BE trong tam giác ABC ta có:
\(\dfrac{AB}{BC}=\dfrac{AE}{CE}=\dfrac{AF+FE}{CE}\)
=> \(\dfrac{a}{b}=\dfrac{x+m}{x}=>x=\dfrac{mb}{a-b}\)= \(\dfrac{3,45.7,25}{12,5-7,25}=\dfrac{667}{140}\)
=> AC = \(2x+m=2.\dfrac{667}{140}+3,45=\dfrac{1817}{140}\approx12,98\)
Vậy AC \(\approx12,98\) cm.

1. Ta có tam giác ABC cân tại A, do đó AB = AC.
Gọi I là giao điểm của đường phân giác góc B và đường phân giác góc C.
Ta cần chứng minh MN // BC.
Ta có:
∠BIM = ∠CIM (do I nằm trên đường phân giác góc B và đường phân giác góc C)
∠BIM = ∠CIM = ∠BIC/2 (do I nằm trên đường phân giác góc B và đường phân giác góc C)
∠BIC = ∠BAC (do tam giác ABC cân tại A)
∠BIC = ∠BAC = ∠BCA (do tam giác ABC cân tại A)
Do đó, ta có ∠BIM = ∠CIM = ∠BCA.
Từ đó, ta có MN // BC (do ∠MNI = ∠BCA và ∠MIN = ∠BAC).
Vậy ta đã chứng minh MN // BC.
2. a) Ta có BF/BE = 2/3.
Gọi x là độ dài của BE.
Do BF/BE = 2/3, ta có BF = (2/3)x.
Gọi y là độ dài của FE.
Do FE = 12cm, ta có y = 12cm.
Gọi z là độ dài của IF.
Do I là giao điểm của FE và BD, ta có IF/FE = BD/BE.
Do đó, IF/12 = BD/x.
Ta có BD = BC + CD = BC + BA = BC + BE.
Do đó, IF/12 = (BC + BE)/x.
Ta có BF/BE = 2/3, nên BF = (2/3)x.
Do đó, BC = BF + FC = (2/3)x + (1/3)x = x.
Vậy, IF/12 = (x + x)/x = 2.
Từ đó, ta có IF = 2 * 12 = 24cm.
Do đó, IE/IF = BE/FE = x/12.
Vậy, IE/IF = x/12.
b) Giả sử FE = 12cm.
Từ phần a), ta đã tính được IF = 24cm.
Do đó, IE/IF = x/12.
Ta cần tính x.
Ta có BF/BE = 2/3, nên BF = (2/3)x.
Do BF = (2/3)x và BC = x, ta có BC = BF + FC.
Do đó, x = (2/3)x + FC.
Từ đó, FC = (1/3)x.
Vậy, BC = BF + FC = (2/3)x + (1/3)x = x.
Do đó, BC = x = 12cm.
Vậy, độ dài của IE và IF lần lượt là 12cm và 24cm.

Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{BD}{4}=\dfrac{CD}{6}\)
mà BD+CD=BC=4cm(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{CD}{6}=\dfrac{BD+CD}{4+6}=\dfrac{4}{10}=\dfrac{2}{5}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{BD}{4}=\dfrac{2}{5}\\\dfrac{CD}{6}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=\dfrac{8}{5}cm\\CD=\dfrac{12}{5}cm\end{matrix}\right.\)
Vậy: \(BD=\dfrac{8}{5}cm;CD=\dfrac{12}{5}cm\)

a; DN\(\perp\)AC
AB\(\perp\)AC
Do đó: DN//AB
=>DN//MB
Xét tứ giác BMND có
BM//DN
BD//MN
Do đó: BMND là hình bình hành
b: Xét ΔABC có
N là trung điểm của AC
NM//BC
Do đó: M là trung điểm của AB
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>\(MN=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)

hướng dẫn thui:
theo tính c hất đường phân giác \(\frac{CN}{AN}=\frac{DC}{AD}=\frac{40.8}{17}\)
\(\frac{AM}{MC}=\frac{AB}{AC}=\frac{40.8}{17}\)\(\Rightarrow\frac{AM}{MC}=\frac{CN}{AN}=\frac{40.8}{17}\)
\(\Rightarrow\frac{AM+MC}{AN+MC}=\frac{40.8}{17}\)\(\Leftrightarrow\frac{2MN+AN+MC}{AN+MC}=\frac{40.8}{17}=\frac{12}{5}\)
\(\frac{2MN}{AC-MN}=\frac{12}{5}-1=\frac{7}{5}\Leftrightarrow\frac{2MN}{\frac{221}{5}-MN}=\frac{7}{5}\)(TÍNH AC DỰA THEO ĐỊNH LÝ PYTAGO)
\(\frac{10}{MN}=839.8-\frac{19}{5}MN\)\(\Rightarrow MN=12.8\left(cm\right)\)