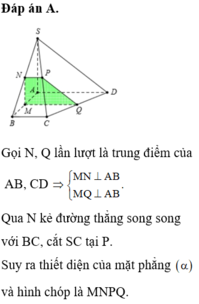
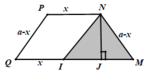
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

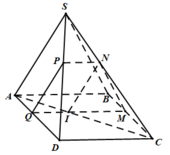
Qua G kẻ đường thẳng d song song với AB.
\(H=d\cap SB;K=d\cap SA\)
Kẻ KP//AD, HT//BC \(\left(P\in SD;T\in SC\right)\)
\(\Rightarrow KHTP\) là thiết diện cần tìm.
\(\dfrac{HK}{AB}=\dfrac{HT}{BC}=\dfrac{KP}{AD}=\dfrac{PT}{CD}=\dfrac{2}{3}\)
Mà \(AB=BC=CD=DA\Rightarrow KH=HT=TP=PK\)
\(\Rightarrow KHPT\) là hình vuông.

Gặp những bài cần tính toán thế này làm biếng lắm, dựng hình thì dễ chứ tính thì chả muốn tính chút xíu nào.
Trong mp đáy, kéo dài AD và BC cắt nhau tại E \(\Rightarrow D\) là trung điểm AE (đường trung bình) \(\Rightarrow AE=AB=2a\)
Ta có: \(\left\{{}\begin{matrix}AD\perp AB\\SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp SB\)
\(\Rightarrow AD\in\left(\alpha\right)\)
Trong mp (SAB), kẻ \(AM\perp SB\Rightarrow M\in\left(\alpha\right)\)
Dễ dàng chứng minh tam giác ACB vuông cân tại C (Pitago đảo) \(\Rightarrow BC\perp\left(SAC\right)\)
Trong mp (SAC), kẻ \(AN\perp SC\Rightarrow AN\perp\left(SBC\right)\Rightarrow AN\perp SB\Rightarrow N\in\left(\alpha\right)\)
\(\Rightarrow\) Thiết diện là tứ giác AMND
\(SB=SE=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(AM=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{AC^2+SA^2}=a\sqrt{3}\)
\(CN=\dfrac{AC^2}{SC}=\dfrac{2a\sqrt{3}}{3}\) ; \(EC=BC=a\sqrt{2}\Rightarrow EN=\sqrt{EC^2+CN^2}=\dfrac{a\sqrt{30}}{3}\)
\(DE=AD=a\)
\(S_{AME}=\dfrac{1}{2}AM.AE=...\)
\(S_{DNE}=\dfrac{1}{2}DE.EN.sin\widehat{DEN}=\dfrac{1}{2}DE.EN.\dfrac{AM}{\sqrt{AM^2+AE^2}}=...\)
\(\Rightarrow S_{AMND}=S_{AME}-S_{DNE}=...\)

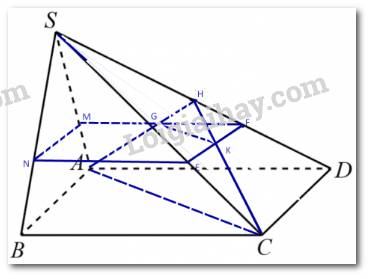
a) Xét tam giác HAC ta có: GH = 2GA, HK = 2KC suy ra GK // AC hay GK // (ABCD).
b) (MNEF) // (ABCD) do đó MN // AB, NE // BC, EF // CD, MF // AD
Lại có AB // CD, AD // BC suy ra MN // EF, MF // NE.
Suy ra, tứ giác MNEF là hình bình hành.