Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.

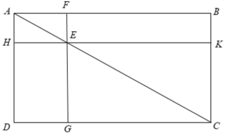
Xem hình 125 ta thấy:
SABC = SADC
SAFE = SAHE
SEKC = SEGC
Suy ra: SABC – SAFE – SEKC = SADC – SAHE - SEGC
hay SEFBK = SEGDH

A F B C D E G
AF // HE ( HK // AB )
AH // EF ( FC // AD )
\(\Rightarrow\)AHEF là hình bình hành
có : góc HAF = 90 độ ( ABCD là hình chữ nhật )
\(\Rightarrow\)AHEF là hình chữ nhật
EF // CG ( HK // AB // CD )
EG // CK ( FG // AD // BC )
\(\Rightarrow\)EGCK là hình bình hành
có góc GCK = 90 độ ( ABCD là hình chữ nhật )
\(\Rightarrow\)EGCK là hình chữ nhật
Ta có : diện tích ABC = 1/2 AB . BC = 1/2diện tích ABCD
diện tích ACD = 1/2 AD . DC = 1/2 diện tích ABCD
\(\Rightarrow\)Diện tích ABC = diện tích ACD
Tương tự : diện tích AEF = diện tích EHA
diện tích ECK = diện tích CFG
diện tích EFBK = diện tích ABC - diện tích AEF - diện tích ECK
diện tích EGDH = diện tích ACD - diện tích EHA - diện CEG
\(\Rightarrow\) diện tích EFBK = diện tích EGDH ( đpcm )

Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
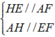 ⇒ AFEH là hình bình hành.
⇒ AFEH là hình bình hành.


a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng

Trả lời:
ABCDMEHKIO
a, Gọi O là giao điểm 2 đường chéo của hình chữ nhật ABCD
=> O là trung điểm của BD và AC
Xét tam giác ACE có:
O là trung điểm của AC
M là trung điểm của AE ( gt )
=> OM là đường trung bình của tam giác ACE
=> OM // CE
hay BD // CE
=> ^BDC = ^ECK ( 2 góc đồng vị ) (1)
Vì O là trung điểm của BD và AC
=> OD = BD/2 và OC = AC/2
Mà BD = AC ( ABCD là hình chữ nhật )
=> OD = OC
=> tam giác DOC cân tại O
=> ^BDC = ^ACD (tc) (2)
Xét tứ giác HEKC có:
^EHC = 90o
^HCK = 90o
^EKC = 90o
=> tứ giác HEKC là hình chữ nhật ( dh1)
Gọi I là giao điểm 2 đường chéo của hình chữ nhật HEKC
=> I là trung điểm của CE và HK
=> IC = CE/2 và IK = HK/2
Mà CE = HK ( HEKC là hình chữ nhật )
=> IC = IK
=> tam giác ICK cân tại I
=> ^ECK = ^IKC (tc) (3)
Từ (1) (2) và (3) => ^ACD = ^IKC
Mà 2 góc này ở vị trí đồng vị
nên AC // HK ( đpcm )
b, Xét tam giác ACE có:
I là trung điểm của CE
M là trung điểm của AE (gt)
=> IM là đường trung bình của tam giác ACE
=> IM // AC
Mà HK // AC ( cm ở ý a ) và H, I, K thẳng hàng
nên M, H, K thẳng hàng ( đpcm )
k nha đúng
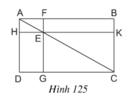
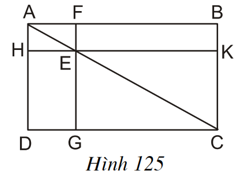
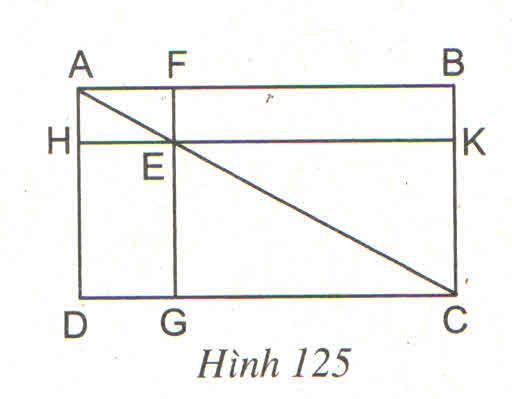
ta có:
SABC = SADC
SAFE = SAHE
SEKC = SEGC
=> SABC – SAFE – SEKC = SADC – SAHE - SEGC
hay SEFBK = SEGDH