Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hàm số y=f(x)y=f(x) có đạo hàm và liên tục trên [0;π2][0;π2]thoả mãn f(x)=f′(x)−2cosxf(x)=f′(x)−2cosx. Biết f(π2)=1f(π2)=1, tính giá trị f(π3)f(π3)
A. √3+1/2 B. √3−1/2 C. 1−√3/2 D. 0

Khi gặp dạng này, ý tưởng là sẽ tìm 1 hàm u(x) sao cho:
\(\int\limits^b_a\left[f'\left(x\right)-u\left(x\right)\right]^2dx=0\) (1)
\(\Rightarrow f'\left(x\right)-u\left(x\right)=0\Rightarrow f'\left(x\right)=u\left(x\right)\)
Khai triển (1), đề cho sẵn \(\left[f'\left(x\right)\right]^2\) nên đại lượng \(2u\left(x\right).f'\left(x\right)\) và hàm \(u\left(x\right)\) sẽ được suy ra từ việc tích phân từng phần \(\int\limits f\left(x\right)dx\). Cụ thể:
Xét \(I=\dfrac{2}{3}=\int\limits^2_0f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.f\left(x\right)|^2_0-\int\limits^2_0xf'\left(x\right)dx=2-\int\limits^2_0xf'\left(x\right)dx\)
\(\Rightarrow\int\limits^2_0xf'\left(x\right)dx=2-\dfrac{2}{3}=\dfrac{4}{3}\) (2)
(Vậy đến đây hàm \(u\left(x\right)\) được xác định là dạng \(u\left(x\right)=k.x\)
Để tìm cụ thể giá trị k:
Từ (1) ta suy luận tiếp:
\(\int\limits^2_0\left[f'\left(x\right)-kx\right]^2dx=0\Leftrightarrow\int\limits^2_0\left[f'\left(x\right)\right]^2-2k\int\limits^2_0x.f'\left(x\right)dx+\int\limits^2_0k^2x^2dx=0\)
\(\Leftrightarrow\dfrac{2}{3}-2k.\dfrac{4}{3}+\dfrac{8}{3}k^2=0\) do \(\int\limits^2_0x^2dx=\dfrac{8}{3}\)
\(\Rightarrow k=\dfrac{1}{2}\)
\(\Rightarrow u\left(x\right)=\dfrac{1}{2}x\) coi như xong bài toán)
Do đó ta có:
\(\int\limits^2_0\left[f'\left(x\right)\right]^2-\int\limits^2_0xf'\left(x\right)+\dfrac{1}{4}\int\limits^2_0x^2dx=\dfrac{2}{3}-\dfrac{4}{3}+\dfrac{1}{4}.\dfrac{8}{3}=0\)
\(\Rightarrow\int\limits^2_0\left[f'\left(x\right)-\dfrac{1}{2}x\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)-\dfrac{1}{2}x=0\)
\(\Rightarrow f'\left(x\right)=\dfrac{1}{2}x\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2+C\)
Thay \(x=2\Rightarrow1=1+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2\)

Vẫn là đạo hàm của tích
Dễ dàng viết được:
\(\left[f'\left(x\right)\right]^2+f\left(x\right).f''\left(x\right)=\left[f\left(x\right)\right]'.f'\left(x\right)+f\left(x\right).\left[f'\left(x\right)\right]'=\left[f'\left(x\right).f\left(x\right)\right]'\)
Do đó giả thiết biến đổi thành:
\(\left[f'\left(x\right).f\left(x\right)\right]'=15x^4+12x\)
Nguyên hàm 2 vế:
\(f'\left(x\right).f\left(x\right)=\int\left(15x^4+12x\right)dx=3x^5+6x^2+C\)
Thay \(x=0\)
\(\Rightarrow f'\left(0\right).f\left(0\right)=C\Rightarrow C=1\)
\(\Rightarrow f'\left(x\right).f\left(x\right)=3x^5+6x^2+1\)
Tiếp tục nguyên hàm 2 vế:
\(\int f\left(x\right).f'\left(x\right)dx=\int\left(3x^5+6x^2+1\right)dx\) với chú ý \(\int f\left(x\right).f'\left(x\right)dx=\int f\left(x\right).d\left[f\left(x\right)\right]=\dfrac{1}{2}f^2\left(x\right)+C\)
Nên:
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+C\)
Thay \(x=0\Rightarrow C=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+\dfrac{1}{2}\)
\(\Rightarrow f^2\left(1\right)\)

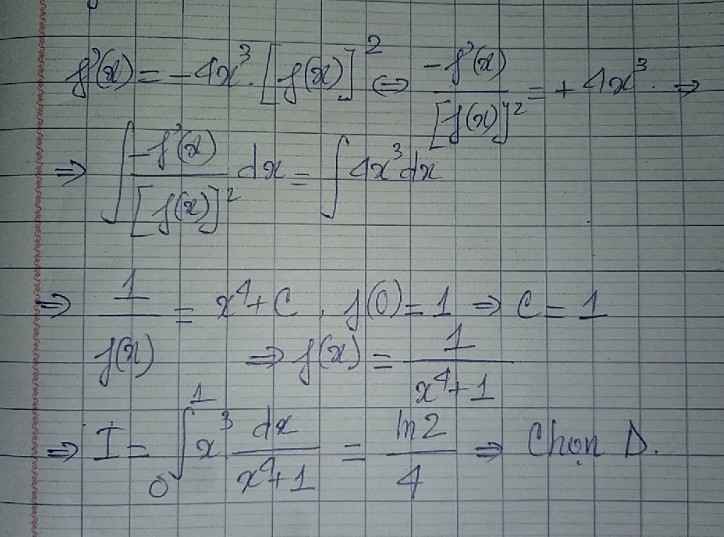


Dạng: \(....f'\left(x\right)+...f\left(x\right)=...\)
Ý tưởng luôn là đưa về đạo hàm của tổng sau đó lấy nguyên hàm 2 vế.
Thêm bớt sao cho vế trái biến thành: \(u\left(x\right).f'\left(x\right)+u'\left(x\right).f\left(x\right)\) là được
So sánh nó với vế trái đề bài, dư ra \(u'\left(x\right)\) ở trước \(f\left(x\right)\) nên ta chia nó (vế kia vẫn ko quan tâm)
Được: \(\dfrac{u\left(x\right)}{u'\left(x\right)}.f'\left(x\right)+f\left(x\right)\)
So sánh nó với đề bài, vậy ta cần tìm hàm \(u\left(x\right)\) sao cho:
\(\dfrac{u\left(x\right)}{u'\left(x\right)}=x\left(x+1\right)\)
Nhưng để thế này ko lấy nguyên hàm được, phải nghịch đảo 2 vế:
\(\dfrac{u'\left(x\right)}{u\left(x\right)}=\dfrac{1}{x\left(x+1\right)}\)
Giờ thì lấy nguyên hàm: \(\int\dfrac{u'\left(x\right)}{u\left(x\right)}dx=\int\dfrac{dx}{x\left(x+1\right)}\Leftrightarrow ln\left|u\left(x\right)\right|=ln\left|\dfrac{x}{x+1}\right|+C\)
Tới đây suy được \(u\left(x\right)=\dfrac{x}{x+1}\) \(\Rightarrow\) vế trái cần có dạng:
\(\dfrac{x}{x+1}f'\left(x\right)+\dfrac{1}{\left(x+1\right)^2}f\left(x\right)\)
Nhìn vào đây là xong rồi. Bài toán sẽ được giải như sau:
Chia 2 vế giả thiết cho \(\left(x+1\right)^2\):
\(\Rightarrow\dfrac{x}{x+1}f'\left(x\right)+\dfrac{1}{\left(x+1\right)^2}f\left(x\right)=\dfrac{x}{x+1}\)
\(\Leftrightarrow\left(\dfrac{x}{x+1}+f\left(x\right)\right)'=\dfrac{x}{x+1}\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow\dfrac{x}{x+1}+f\left(x\right)=\int\dfrac{x}{x+1}dx=\int\left(1-\dfrac{1}{x+1}\right)dx=x-ln\left|x+1\right|+C\)
\(\Rightarrow f\left(x\right)=x-\dfrac{x}{x+1}-ln\left|x+1\right|+C=\dfrac{x^2}{x+1}-ln\left|x+1\right|+C\)
Thay \(x=1\)
\(\Rightarrow f\left(1\right)=\dfrac{1}{2}-ln2+C\Rightarrow-2ln2=\dfrac{1}{2}-ln2+C\)
\(\Rightarrow C=-ln2-\dfrac{1}{2}\)
\(\Rightarrow f\left(x\right)=\dfrac{x^2}{x+1}-ln\left|x+1\right|-ln2-\dfrac{1}{2}\)
\(\Rightarrow f\left(2\right)=...\)