
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

Ta có
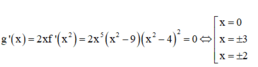
Bảng biến thiên của hàm số y= g( x)
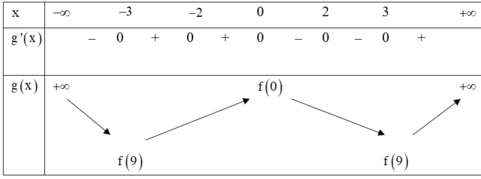
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.


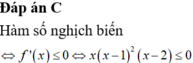
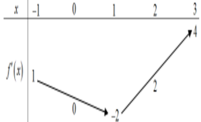
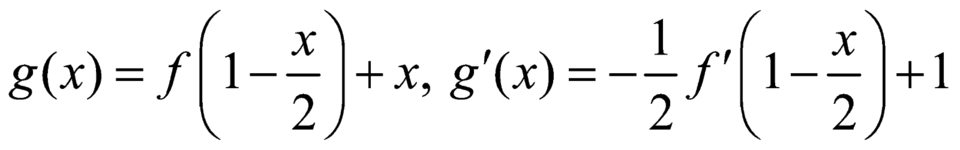
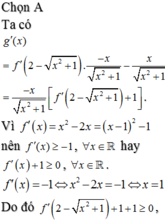
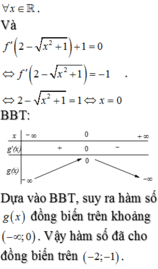
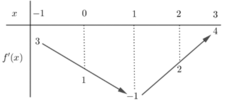

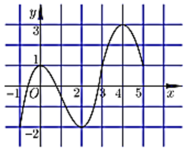

\(y=f\left(x\right)=\left(x-1\right)\left(2x-3\right)\) đồng biến khi: \(\left(x-1\right)\left(2x-3\right)>0\)
\(\Leftrightarrow x-1>0;2x-3>0\) hoặc \(x-1< 0;2x-3< 0\)
\(\Leftrightarrow x>1;x>\frac{3}{2}\) hoặc \(x< 1;x< \frac{3}{2}\)
\(\Leftrightarrow x>\frac{3}{2}\) hoặc \(x< 1\)
\(y=f\left(x\right)=\left(x-1\right)\left(2x-3\right)\) nghịch biến khi: \(\left(x-1\right)\left(2x-3\right)< 0\)
\(\Leftrightarrow x-1>0;2x-3< 0\) hoặc \(x-1< 0;2x-3>0\)
\(\Leftrightarrow x>1;x< \frac{3}{2}\) hoặc \(x< 1;x>\frac{3}{2}\)
\(\Leftrightarrow1< x< \frac{3}{2}\)