Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Tọa độ giao điểm là:
-3x+5=2x và y=2x
=>-5x=-5 và y=2x
=>x=1 và y=2
c: Ox: y=0
Vì (d): y=ax+b song song với Ox: y=0x+0 nên a=0
=>y=b
Thay x=0 và y=4 vào y=b, ta được:
b=4
=>y=4
Tọa độ P là:
2x=4 và y=4
=>x=2 và y=4
Tọa độ Q là:
-3x+5=4 và y=4
=>-3x=-1 và y=4
=>x=1/3 và y=4

b. Đồ thị đt đề cho là y=6
PTGD 2 đt đầu bài với đt câu b là: \(\left\{{}\begin{matrix}2x=6\\x-1=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\rightarrow A\left(3;6\right)\\x=7\rightarrow B\left(7;6\right)\end{matrix}\right.\)

a) 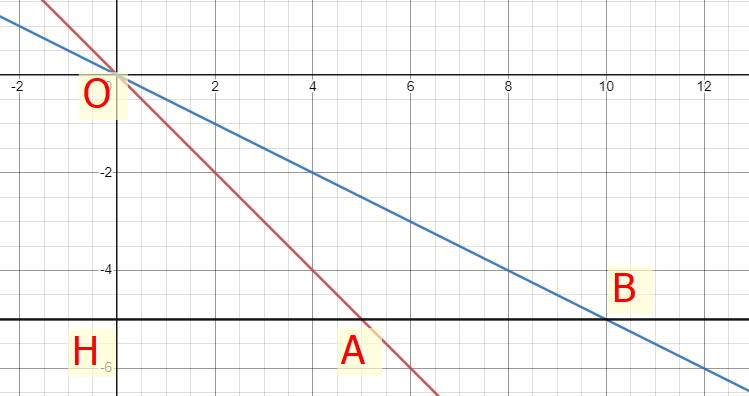
b) Ta có đường thẳng đi qua điểm H(0;-5) nên phương trình đường thẳng đi qua H là:
\(y=0x-5\Rightarrow y=-5\)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-x\) là:
\(-5=-x\)
\(\Rightarrow x=5\)
Tọa độ điểm A là (5;-5)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-\dfrac{1}{2}x\) là:
\(-5=-\dfrac{1}{2}x\)
\(\Rightarrow\dfrac{1}{2}x=5\)
\(\Rightarrow x=5:\dfrac{1}{2}\)
\(\Rightarrow x=10\)
Tọa độ điểm B là (10;-5)
c) Ta có: A(5;-5) và B(10;-5)
Độ dài đường thẳng AB là \(10-5=5\left(đvđd\right)\)
Có A(5;-5) ⇒ HA = 5 (đvđd)
Xét tam giác OHA vuông tại H áp dụng định lý Py-ta-go ta có:
\(OA^2=HA^2+OH^2\) (tọa độ điểm H(0;-5) nên OH = 5 đvđd)
\(\Rightarrow OA=\sqrt{5^2+5^2}=\sqrt{50}=5\sqrt{2}\left(đvđd\right)\)
Có B(10;-5) ⇒ HB = 10 (đvđd)
Xét tam giác OHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(OB^2=HB^2+OH^2\)
\(\Rightarrow OB=\sqrt{10^2+5^2}=\sqrt{125}=5\sqrt{5}\left(đvđd\right)\)
Chu vi: \(C_{OAB}=AB+OA+OB=5+5\sqrt{2}+5\sqrt{5}\approx23,25\left(đvđd\right)\)
Diện tích: \(S_{OAB}=\dfrac{1}{2}\cdot OH\cdot AB=\dfrac{1}{2}\cdot5\cdot5=12,5\left(đvdt\right)\)