Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đk: \(k\ge0\)
a)
A(0,2\(\sqrt{3}\))
x=0
\(\Rightarrow y=\sqrt{k}+\sqrt{3}\)
\(\Rightarrow\sqrt{k}=2\sqrt{3}-\sqrt{3}=\sqrt{3}\)
\(\Rightarrow k=3\) nhận
b)
\(B\left(1;0\right)\)
\(\Leftrightarrow\dfrac{\sqrt{k}+1}{\sqrt{3}-1}.1+\sqrt{k}+\sqrt{3}=0\)
\(\Leftrightarrow\sqrt{k}+1+\sqrt{k}.\left(\sqrt{3}-1\right)+\sqrt{3}\left(\sqrt{3}-1\right)=0\)
\(\Leftrightarrow\sqrt{3}\sqrt{k}+4-\sqrt{3}=0\)
\(4>\sqrt{3}\Rightarrow Vo..N_0\)
(d) không đi qua điểm B(1;0)
c) Sửa đề \(k\ge0\)
\(\Leftrightarrow y=\dfrac{\sqrt{k}.x+x+\sqrt{3}\sqrt{k}-\sqrt{k}+\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(\Leftrightarrow y=\dfrac{\sqrt{k}\left(x+\sqrt{3}-1\right)+x+\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
Với \(x=1-\sqrt{3}\) => y=\(\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{3}-1\) không phụ thuộc k
Điểm cố định
D\(\left(\left(1-\sqrt{3}\right);\left(\sqrt{3}+1\right)\right)\)

a) Vẽ đồ thị
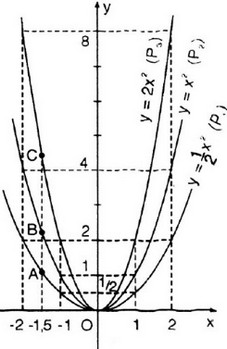
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA =  . (-1,5)2 =
. (-1,5)2 =  . 2,25 = 1,125
. 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, =  . 1,52 =
. 1,52 =  . 2,25 = 1,125
. 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.
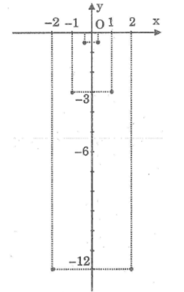









a: Khi x=-2 thì \(y=-3\cdot\left(-2\right)^2=-12\)
Khi x=-1 thì \(y=-3\cdot\left(-1\right)^2=-3\)
Khi x=-1/3 thì \(y=-3\cdot\dfrac{1}{9}=-\dfrac{1}{3}\)
Khi x=0 thì y=0
Khi x=1/3 thì \(y=-3\cdot\dfrac{1}{9}=-\dfrac{1}{3}\)
Khi x=1 thì y=-3
Khi x=2 thì y=-12
b: