Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có : \(10=\int ^{3}_{1}f(2x)dx=\frac{1}{2}\int ^{3}_{1}f(2x)d(2x)=\frac{1}{2}\int ^{6}_{2}f(x)dx\)
\(\Rightarrow \int ^{6}_{2}f(x)d(x)=20\)
Mà \(\int ^{2}_{0}f(x)dx=-5\Rightarrow \int ^{6}_{0}f(x)dx=15\)
Do đó mà \(\int ^{2}_{0}f(3x)dx=\frac{1}{3}\int ^{2}_{0}f(3x)d(3x)=\frac{1}{3}\int ^{6}_{0}f(x)dx=5\)

\(\int\limits^3_{-1}f\left(\left|x\right|\right)dx=\int\limits^0_{-1}f\left(\left|x\right|\right)dx+\int\limits^1_0f\left(\left|x\right|\right)dx+\int\limits^3_1f\left(\left|x\right|\right)dx\)
\(=\int\limits^0_{-1}f\left(-x\right)dx+\int\limits^1_0f\left(x\right)dx+\int\limits^3_1f\left(x\right)dx\)
\(=\int\limits^1_0f\left(x\right)dx+\int\limits^1_0f\left(x\right)dx+\int\limits^3_1f\left(x\right)dx\)
\(=3+3+6=12\)

Khi gặp dạng này, ý tưởng là sẽ tìm 1 hàm u(x) sao cho:
\(\int\limits^b_a\left[f'\left(x\right)-u\left(x\right)\right]^2dx=0\) (1)
\(\Rightarrow f'\left(x\right)-u\left(x\right)=0\Rightarrow f'\left(x\right)=u\left(x\right)\)
Khai triển (1), đề cho sẵn \(\left[f'\left(x\right)\right]^2\) nên đại lượng \(2u\left(x\right).f'\left(x\right)\) và hàm \(u\left(x\right)\) sẽ được suy ra từ việc tích phân từng phần \(\int\limits f\left(x\right)dx\). Cụ thể:
Xét \(I=\dfrac{2}{3}=\int\limits^2_0f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.f\left(x\right)|^2_0-\int\limits^2_0xf'\left(x\right)dx=2-\int\limits^2_0xf'\left(x\right)dx\)
\(\Rightarrow\int\limits^2_0xf'\left(x\right)dx=2-\dfrac{2}{3}=\dfrac{4}{3}\) (2)
(Vậy đến đây hàm \(u\left(x\right)\) được xác định là dạng \(u\left(x\right)=k.x\)
Để tìm cụ thể giá trị k:
Từ (1) ta suy luận tiếp:
\(\int\limits^2_0\left[f'\left(x\right)-kx\right]^2dx=0\Leftrightarrow\int\limits^2_0\left[f'\left(x\right)\right]^2-2k\int\limits^2_0x.f'\left(x\right)dx+\int\limits^2_0k^2x^2dx=0\)
\(\Leftrightarrow\dfrac{2}{3}-2k.\dfrac{4}{3}+\dfrac{8}{3}k^2=0\) do \(\int\limits^2_0x^2dx=\dfrac{8}{3}\)
\(\Rightarrow k=\dfrac{1}{2}\)
\(\Rightarrow u\left(x\right)=\dfrac{1}{2}x\) coi như xong bài toán)
Do đó ta có:
\(\int\limits^2_0\left[f'\left(x\right)\right]^2-\int\limits^2_0xf'\left(x\right)+\dfrac{1}{4}\int\limits^2_0x^2dx=\dfrac{2}{3}-\dfrac{4}{3}+\dfrac{1}{4}.\dfrac{8}{3}=0\)
\(\Rightarrow\int\limits^2_0\left[f'\left(x\right)-\dfrac{1}{2}x\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)-\dfrac{1}{2}x=0\)
\(\Rightarrow f'\left(x\right)=\dfrac{1}{2}x\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2+C\)
Thay \(x=2\Rightarrow1=1+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2\)

Xét \(I=\int\limits^1_0x^2f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=x^2dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{1}{3}x^3\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{3}x^3.f\left(x\right)|^1_0-\dfrac{1}{3}\int\limits^1_0x^3.f'\left(x\right)dx=-\dfrac{1}{3}\int\limits^1_0x^3f'\left(x\right)dx\)
\(\Rightarrow\int\limits^1_0x^3f'\left(x\right)dx=-1\)
Lại có: \(\int\limits^1_0x^6.dx=\dfrac{1}{7}\)
\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+14\int\limits^1_0x^3.f'\left(x\right)dx+49.\int\limits^1_0x^6dx=0\)
\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)+7x^3\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)+7x^3=0\)
\(\Rightarrow f'\left(x\right)=-7x^3\)
\(\Rightarrow f\left(x\right)=\int-7x^3dx=-\dfrac{7}{4}x^4+C\)
\(f\left(1\right)=0\Rightarrow C=\dfrac{7}{4}\)
\(\Rightarrow I=\int\limits^1_0\left(-\dfrac{7}{4}x^4+\dfrac{7}{4}\right)dx=...\)

Tham khảo:
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
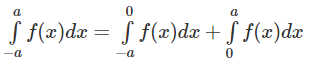
Đổi biến x = - t đối với tích phân
Ta được:
Vậy
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì
là hàm số lẻ trên đoạn [-2; 2] nên

2a. Đề sai, nhìn biểu thức \(\dfrac{f'\left(x\right)}{f'\left(x\right)}dx\) là thấy
2b. Đồ thị hàm số không cắt Ox trên \(\left(0;1\right)\) nên diện tích cần tìm:
\(S=\int\limits^1_0\left(x^4-5x^2+4\right)dx=\dfrac{38}{15}\)
3a. Phương trình (P) theo đoạn chắn:
\(\dfrac{x}{4}+\dfrac{y}{-1}+\dfrac{z}{-2}=1\)
3b. Câu này đề sai, đề cho mặt phẳng (Q) rồi thì sao lại còn viết pt mặt phẳng (Q) nữa?
sorry thầy em xin sửa lại câu 3 b là
b) trong không gian Oxyz cho mặt phẳng (Q): 3x-y-2z+1=0.Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q) và đi qua điểm M(0;0;1)

1/ \(I=\int\limits^1_0\dfrac{2x+1}{x^2+x+1}dx=\int\limits^1_0\dfrac{d\left(x^2+x+1\right)}{x^2+x+1}=ln\left|x^2+x+1\right||^1_0=ln3\)
2/ \(\int\limits^{\dfrac{1}{2}}_0\dfrac{5x}{\left(1-x^2\right)^3}dx=-\dfrac{5}{2}\int\limits^{\dfrac{1}{2}}_0\dfrac{d\left(1-x^2\right)}{\left(1-x^2\right)^3}=\dfrac{5}{4}\dfrac{1}{\left(1-x^2\right)^2}|^{\dfrac{1}{2}}_0=\dfrac{35}{36}\)
3/ \(\int\limits^1_0\dfrac{2x}{\left(x+1\right)^3}dx\Rightarrow\) đặt \(x+1=t\Rightarrow x=t-1\Rightarrow dx=dt;\left\{{}\begin{matrix}x=0\Rightarrow t=1\\x=1\Rightarrow t=2\end{matrix}\right.\)
\(I=\int\limits^2_1\dfrac{2\left(t-1\right)dt}{t^3}=\int\limits^2_1\left(\dfrac{2}{t^2}-\dfrac{2}{t^3}\right)dt=\left(\dfrac{-2}{t}+\dfrac{1}{t^2}\right)|^2_1=\dfrac{1}{4}\)
4/ \(\int\limits^1_0\dfrac{4x-2}{\left(x^2+1\right)\left(x+2\right)}dx\)
Kĩ thuật chung là tách và sử dụng hệ số bất định như sau:
\(\dfrac{4x-2}{\left(x^2+1\right)\left(x+2\right)}=\dfrac{ax+b}{x^2+1}+\dfrac{c}{x+2}=\dfrac{\left(a+c\right)x^2+\left(2a+b\right)x+2b+c}{\left(x^2+1\right)\left(x+2\right)}\)
\(\Rightarrow\left\{{}\begin{matrix}a+c=0\\2a+b=4\\2b+c=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=0\\a=-c=2\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^1_0\left(\dfrac{2x}{x^2+1}-\dfrac{2}{x+2}\right)dx=\int\limits^1_0\dfrac{d\left(x^2+1\right)}{x^2+1}-2\int\limits^1_0\dfrac{d\left(x+2\right)}{x+2}=ln\dfrac{8}{9}\)
5/ \(\int\limits^1_0\dfrac{x^2dx}{x^6-9}\Rightarrow\) đặt \(x^3=t\Rightarrow3x^2dx=dt\Rightarrow x^2dx=\dfrac{1}{3}dt;\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=1\Rightarrow t=1\end{matrix}\right.\)
\(I=\dfrac{1}{3}\int\limits^1_0\dfrac{dt}{t^2-9}=\dfrac{1}{18}\int\limits^1_0\left(\dfrac{1}{t-3}-\dfrac{1}{t+3}\right)dt=\dfrac{1}{18}ln\left|\dfrac{t-3}{t+3}\right||^1_0=-\dfrac{1}{18}ln2\)
6/ Tương tự câu 4, sử dụng hệ số bất định ta tách được:
\(\int\limits^2_1\dfrac{2x-1}{x^2\left(x+1\right)}dx=\int\limits^2_1\left(\dfrac{3x-1}{x^2}-\dfrac{3}{x+1}\right)dx=\int\limits^2_1\left(\dfrac{3}{x}-\dfrac{1}{x^2}-\dfrac{3}{x+1}\right)dx\)
\(=\left(3ln\left|\dfrac{x}{x+1}\right|+\dfrac{1}{x}\right)|^2_1=3ln\dfrac{4}{3}-\dfrac{1}{2}\)
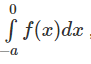
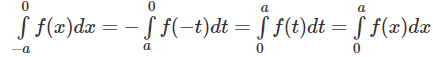
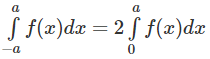
Đặt \(2x+2=u\Rightarrow2xdx=du\Rightarrow dx=\dfrac{1}{2}du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=2\\x=2\Rightarrow u=6\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^6_2f\left(u\right).\dfrac{1}{2}du=\dfrac{1}{2}\int\limits^6_2f\left(u\right)du=\dfrac{1}{2}\int\limits^6_2f\left(x\right)dx=\dfrac{1}{2}.6=3\)