Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Q=\dfrac{2002}{a}+\dfrac{2017}{b}+2996a-5501b=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-\left(5012a+7518b\right)\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-2506\left(2a+3b\right)\)
Áp dụng bất đẳng thức Cosi cho 2 số dương:
\(\left\{{}\begin{matrix}\dfrac{2002}{a}+8008\ge2\sqrt{\dfrac{2002}{a}.8008}=8008\\\dfrac{2017}{b}+2017b\ge2\sqrt{\dfrac{2017}{b}.2017b}=4034\end{matrix}\right.\)
Ta có: \(2a+3b=4\Rightarrow-\left(2a+3b\right)=-4\Leftrightarrow-2506\left(2a+3b\right)=-10024\)
\(\Rightarrow Q\ge8008+4034-10024=2018\)
\(ĐTXR\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)

Chào bạn, mình từng làm bài này giúp một bạn khác rồi, link đây nhé:
https://hoc24.vn/hoi-dap/question/778686.html

\(Q=\frac{2002}{a}+8008a+\frac{2017}{b}+2017b-2506\left(2a+3b\right)\)
\(Q\ge2\sqrt{\frac{2002}{a}.8008a}+2\sqrt{\frac{2017}{b}.2017b}-2506.4\)
\(Q\ge2018\)
\(\Rightarrow Q_{min}=2018\) khi \(\left\{{}\begin{matrix}a=\frac{1}{2}\\b=1\end{matrix}\right.\)


Ta có
Q = 2002 1 a + 4 a + 2017 1 b + b − 5012 a − 7518 b = 2002 1 a + 4 a + 2017 1 b + b − 2506 2 a + 3 b
+ Vì a, b dương và 2 a + 3 b ≤ 4 ⇒ 0 < 2 a + 3 b ≤ 4 do đó
Q ≥ 2002.2. 1 a .4 a + 2017.2. 1 b . b − 2506.4 = 2018 với mọi a, b>0 và 2 a + 3 b ≤ 4 , dấu bằng xảy ra khi a = 1 2 và b= 1.
+ Vậy giá trị nhỏ nhất của Q bằng 2018 khi a = 1 2 và b= 1..

1) Ta có ĐK: 0 < a,b,c < 1
\(\sqrt{\frac{a}{1-a}}=\frac{a}{\sqrt{a\left(1-a\right)}}\ge2a\) (BĐT AM-GM cho 2 số a và 1-a)
Tương tự, ta có \(\sqrt{\frac{b}{1-b}}=\frac{b}{\sqrt{b\left(1-b\right)}}\ge2b\) và \(\sqrt{\frac{c}{1-c}}=\frac{c}{\sqrt{c\left(1-c\right)}}\ge2c\)
⇒ \(\sqrt{\frac{a}{1-a}}+\sqrt{\frac{b}{1-b}}+\sqrt{\frac{c}{1-c}}\ge2\left(a+b+c\right)=2\)(do a+b+c=1)
Dấu đẳng thức xảy ra \(\Leftrightarrow\) a = b = c = \(\frac{1}{2}\) (không thoả mãn điều kiện a+b+c=1)
Dấu đẳng thức trên không xảy ra được. Vậy ta có bất đẳng thức\(\sqrt{\frac{a}{1-a}}+\sqrt{\frac{b}{1-b}}+\sqrt{\frac{c}{1-c}}>2\)
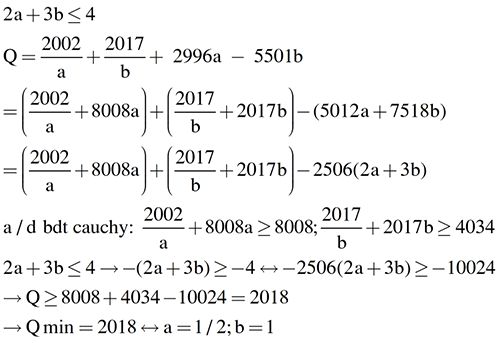
Ta có:
\(Q=\dfrac{2002}{a}+\dfrac{2017}{b}+2996a-5501b\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-\left(5012a+7518b\right)\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-2506\left(2a+3b\right)\)
Áp dụng BĐT Cauchy cho hai số không âm ta có:
\(\dfrac{2002}{a}+8008a\ge2\sqrt{\dfrac{2002}{a}.8008a}=2.4004=8008\) (1)
\(\dfrac{2017}{b}+2017b\ge2\sqrt{\dfrac{2017}{b}.2017b}=2.2017=4034\) (2)
Có \(2a+3b\le4\Rightarrow-\left(2a+3b\right)\ge-4\Rightarrow-2506\left(2a+3b\right)\ge-10024\)(3)
Từ (1), (2) và (3) \(\Rightarrow Q\ge8008+4034-10024=2018\)
Dấu '=' xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2002}{a}=8008a\\\dfrac{2017}{b}=2017b\\2a+3b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)
Vậy,...