Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số điểm cực đại trên đoạn AG là số giá trị k thỏa mãn \(-AG \leq (k+\frac{\triangle \phi}{2\pi})\lambda \leq AG \Rightarrow -\frac{AB}{4}.3=10.875cm \leq (k+0.5)\lambda \leq 10.875\\ \Rightarrow -5.94 \leq k \leq 4.94 \Rightarrow k = -5,-4,\ldots,0,1,\ldots,4\)
có 10 điểm dao động cực đại trên đoạn AG

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Tại P dao động cực tiểu khi \(d_{2}-d_{1}=(2k+1+\frac{\triangle \phi}{\pi})\frac{\lambda}{2}.\)
Tại P dao động cực đại khi \(d_{2}-d_{1}=(k+\frac{\triangle \phi}{2\pi})\lambda.\)
Tại M là vân lồi bậc k và tại N là vân lồi bậc k + 3 =>\(MA-MB=(k+0.5)\lambda=12.25\\ NA-NB=(k+3+0.5)\lambda=33.25\\ \)
\(\Rightarrow 3\lambda=33.25-12.25=21 \Rightarrow \lambda=7mm.\)
Số điểm cực đại giao thoa trên đoạn AB là \(-AB\leq (k+\frac{1}{2})\lambda\leq AB \Rightarrow \frac{-AB}{\lambda}-0.5 \leq k \leq \frac{AB}{\lambda}\)
=> có 14 điểm cực đại giao thoa kể cả A và B.

\(\lambda=\frac{v}{f}=\frac{10}{5}=2cm.\)
- Điểm P thuộc MI có:
\(u_P=2a\cos2\pi(ft-\frac{d_1}{\lambda})\)
\(u_I=2a\cos2\pi(ft-\frac{d_1}{\lambda})\)
=> độ lệch pha giữa P và I là: \(\triangle \phi = 2\pi \frac{d_1-d_1^{'}}{\lambda}\)
- Điểm P đồng pha với điểm I khi
\(\triangle\phi=2\pi\frac{d_1-d_1^{'}}{\lambda}=2k\pi.\)
\(\Rightarrow d_1-d_1^{'}=k\lambda\)
\( mà \ \ O_1I-O_1I< d_1-d_1^{'}< O_1M-O_1I (1)\\ \Rightarrow 0< k<\frac{10\sqrt2-10}{2}=2.07\\ \Rightarrow k = 1;2. \)
=> có 2 điểm trên khoảng MI đồng pha với điểm I.
- Điểm P ngược pha với điểm I khi \(\triangle\phi=2\pi\frac{d_1-d_1^{'}}{\lambda}=(2k+1)\pi.\)
Dựa vào phương trình (1) ta tìm được k = 0,1.=> có 2 điểm trên khoảng MI ngược pha với điểm I.
Điểm P vuông pha với điểm I khi \(\triangle\phi=2\pi\frac{d_1-d_1^{'}}{\lambda}=k\pi+\frac{\pi}{2}.\)
Dựa vào phương trình (1) ta tìm được k = 0,1,2,3. => có 4 điểm trên khoảng MI vuông pha với điểm I.

Chọn đáp án B
I năm trên trung trực của AB =>> IOA vuông tai O.mà I cùng pha với A,B =>> IA=IB=kλ =8k I gần o nhất.mà OA=10 =>> k=2 tm =>> IA=16 =>> IO^2=IA^2-OA^2=16^2-10^2=156 => IO=căn 156 =>> B đúng


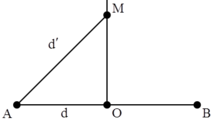

\(\lambda =\frac{v}{f}=\frac{50}{10}=5cm.\)
Điểm M ngược pha với điểm I khi: \(\triangle \phi=\phi_I-\phi_M = 2\pi \frac{d_1-d_{1}^{'}}{\lambda}=(2k+1)\pi \Rightarrow d_1-d_1^{'}=(2k+1)\frac{\lambda}{2}\)
Để điểm M gần I nhất thì hiệu d1 - d1' cũng phải nhỏ nhất khi đó k chỉ nhận giá trị nhỏ nhất là k = 0.
\(d_{1}-d_{1}^{'}=(2.0+1)\frac{5}{2}=2.5cm\Rightarrow d_1 = 7.5cm.\)
\(\Rightarrow MI= \sqrt {d_1^{2}-d_1^{'2}}\) = \(\sqrt{7.5^2-2.5^2}=\sqrt{50}cm\)