Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ sau:
K B A C 1 2 O
a) Vì AB = AC => ΔABC cân => \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABO và ΔACO có:
AO: cạnh cung
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
OB = OC (gt)
=> ΔABO = ΔACO (đpcm)
b) Vì AK // BC(gt) => \(\widehat{KAB}=\widehat{ABO}\) (so le trong)
Mà \(\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{KAB}=\widehat{ACB}\) (*)
Vì ΔABO = ΔACO (ý a) => \(\widehat{A_1}=\widehat{A_2}\)
mà \(\widehat{A_1}=\widehat{ABK}\) (so le trong do AK // BC)
=> \(\widehat{A_2}=\widehat{ABK}\) (**)
Xét ΔABK và ΔACO có:
\(\widehat{KAB}=\widehat{ACB}\) (*)
AB = AC (gt)
\(\widehat{A_2}=\widehat{ABK}\) (**)
=> ΔABK = ΔACO (g.c.g)
=> AK = OC (đpcm)

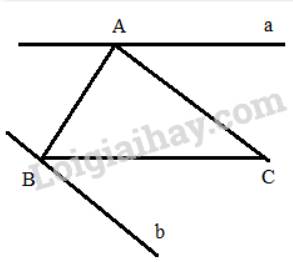
Đo góc ABC. Vẽ đường thẳng a đi qua A sao cho góc tạo bởi a và đường thẳng AB bằng góc ABC.
Ta được đường thẳng a đi qua A và song song với BC
Đo góc ACB. Vẽ đường thẳng b đi qua B sao cho góc tạo bởi b và đường thẳng BC bằng góc ACB.
Ta được đường thẳng b đi qua B và song song với AC
b) Có thể vẽ được chỉ 1 đường thẳng a, 1 đường thẳng b thoả mãn yêu cầu. Vì qua 1 điểm nằm ngoài một đường thẳng, chỉ có 1 đường thẳng song song với nó

a) Xét ∆AMB và ∆AMC có :
BM = MC ( M là trung điểm BC )
AM chung
AB = AC
=> ∆AMB = ∆AMC (c.c.c)
b) Vì AB = AC
=> ∆ABC cân tại A
Mà AM là trung tuyến
=> AM \(\perp\)BC
Mà a\(\perp\)AM
=> a//BC ( từ vuông góc tới song song )
c) Vì CN//AM (gt)
AN//MC ( a//BC , M thuộc BC)
=> ANCM là hình bình hành
=> NC = AM , AN = MC
Mà AMC = 90°
=> ANCM là hình chữ nhật
=> NAM = AMC = MCN = CNA = 90°
Xét ∆ vuông NAC và ∆ vuông MCA có :
AN = MC
AM = CN
=> ∆NAC = ∆MCA (ch-cgv)
d) Vì ANCM là hình chữ nhật (cmt)
=> AC = MN , I là trung điểm 2 đường chéo NM và AC (dpcm)